deep learning book-第2章 Linear Algebra
标签:deep learning book目录
- 2.1 Scalars, Vectors, Matrices and Tensors
- 2.2 Multiplying Matrices and Vectors
- 2.3 Identity and Inverse Matrices
- 2.4 Linear Dependence and Span
- 2.5 Norms
- 2.6 Special Kinds of Matrices and Vectors
- 2.7 Eigendecomposition
- 2.8 Singular Value Decomposition
- 2.9 The Moore-Penrose Pseudoinverse
- 2.10 The Trace Operator
- 2.11 The Determinant
- 2.12 Example: Principal Components Analysis
几个git链接:
- https://github.com/HFTrader/DeepLearningBook
- https://github.com/ExtremeMart/DeepLearningBook-ReadingNotes
- https://github.com/ExtremeMart/DeepLearningBook-CN
目录:
- 2.1 Scalars, Vectors, Matrices and Tensors
- 2.2 Multiplying Matrices and Vectors
- 2.3 Identity and Inverse Matrices
- 2.4 Linear Dependence and Span
- 2.5 Norms
- 2.6 Special Kinds of Matrices and Vectors
- 2.7 Eigendecomposition
- 2.8 Singular Value Decomposition
- 2.9 The Moore-Penrose Pseudoinverse
- 2.10 The Trace Operator
- 2.11 The Determinant
- 2.12 Example: Principal Components Analysis
2.1 Scalars, Vectors, Matrices and Tensors
- Scalars:标量,一个单独的数字。用斜体小写字母表示
\(a,n,x\) - vectors:向量,一个1-D的数组(默认都是列向量!!)。用小写斜体加粗表示
\(\boldsymbol{x}\in \mathbb{R}^n\):
\[
\boldsymbol{x} = \begin{bmatrix}x_1
\\ x_2
\\ ...
\\ x_n
\end{bmatrix}
\]
- matrices:矩阵,一个2-D的数组。用大写斜体加粗表示
\(\boldsymbol{A}\in \mathbb{R}^{m\times n}\):- 矩阵转置,简单理解就是将矩阵沿着主对角线做一次镜像:
\((\boldsymbol{A}^T)_{i,j}=\boldsymbol{A}_{j,i}\)
- 矩阵转置,简单理解就是将矩阵沿着主对角线做一次镜像:
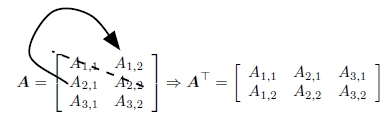
\[
(\boldsymbol{A}\boldsymbol{B})^T=\boldsymbol{B}^T\boldsymbol{A}^T
\]
- tensors:张量:0维==>标量;1维==>向量;2维==>矩阵;可以更多维(用加粗大写非斜体表示)
\(\mathbf{A}\in \mathbb{R}^{i\times j\times k}\)。
2.2 Multiplying Matrices and Vectors
矩阵点积(dot product):
\[
\\\boldsymbol{C}=\boldsymbol{A}\boldsymbol{B}
\\C_{i,j}=\sum _kA_{i,k}B_{k,j}
\]
另外,矩阵的Hadamard product(element-wise product)是对应元素相乘:
\[
\\\boldsymbol{C}=\boldsymbol{A}\odot \boldsymbol{B}
\\C_{i,j}=A_{i,j}B_{k,j}
\]
矩阵的点积具有分配律和结合律:
\[
\\\boldsymbol{A}(\boldsymbol{B}+\boldsymbol{C})=\boldsymbol{A}\boldsymbol{B}+\boldsymbol{A}\boldsymbol{C}
\\(\boldsymbol{A}\boldsymbol{B})\boldsymbol{C}=\boldsymbol{A}(\boldsymbol{B}\boldsymbol{C})
\]
注意,对于向量而言(\(\boldsymbol{x}\)是\(n\times 1\)的列向量,所以\(\boldsymbol{x}^T\)是\(1\times n\)的行向量),所以\(\boldsymbol{x}_T\boldsymbol{y}\)是一个标量,他等于他的转置:
\[
\boldsymbol{x}^T\boldsymbol{y}=(\boldsymbol{x}^T\boldsymbol{y})^T=\boldsymbol{y}^T\boldsymbol{x}
\]
接下来看一下线性方程组(linear equations),\(\boldsymbol{A}\in \mathbb{R}^{m\times n}\)是一个已知的矩阵,\(\boldsymbol{b}\in \mathbb{R}^{m}\)是一个已知的向量,\(\boldsymbol{x}\in \mathbb{R}^{n}\)是一个未知的向量:
\[
\boldsymbol{x}^T\boldsymbol{y}=(\boldsymbol{x}^T\boldsymbol{y})^T=\boldsymbol{y}^T\boldsymbol{x}
\]
等价于
\[
\\\boldsymbol{A}_{1,:}\boldsymbol{x}=\boldsymbol{A}_{1,1}x_1+\boldsymbol{A}_{1,2}x_2+...+\boldsymbol{A}_{1,n}x_n=b1
\\\boldsymbol{A}_{2,:}\boldsymbol{x}=\boldsymbol{A}_{2,1}x_1+\boldsymbol{A}_{2,2}x_2+...+\boldsymbol{A}_{2,n}x_n=b2
\\...
\\\boldsymbol{A}_{m,:}\boldsymbol{x}=\boldsymbol{A}_{m,1}x_1+\boldsymbol{A}_{m,2}x_2+...+\boldsymbol{A}_{m,n}x_n=bm
\]
2.3 Identity and Inverse Matrices
单位矩阵:主对角线全1,其他元素全0的矩阵。单位矩阵和任何向量相乘,结果都是该向量本身。即,\(\boldsymbol{I}_n\in \mathbb{R}_{n\times n}\),有:
\[
\forall \boldsymbol{x}\in \mathbb{R}_{n},\ \boldsymbol{I}_n\boldsymbol{x}=\boldsymbol{x}
\]
矩阵的逆:\(\boldsymbol{A}^{-1}\)满足:\(\boldsymbol{A}^{-1}\boldsymbol{A}=\boldsymbol{I}_n\)
所以可以对方程组进行求解:\(\boldsymbol{x}=\boldsymbol{A}^-1\boldsymbol{b}\)
2.4 Linear Dependence and Span
线性方程组的解只有以下三种情况:
- 无解
- 有无穷多的解:
\(\boldsymbol{x}\)和\(\boldsymbol{y}\)都是解,那么\(\boldsymbol{z}=\alpha \boldsymbol{x}+(1-\alpha )\boldsymbol{y}\)也是解 - 只有一个解
为了分析方程组有多少个解,我们可以从这个角度来理解线性方程组:我们从m维零向量出发,经过\(\boldsymbol{A}\)的n个方向的变换,最终到达m维目标向量\(\boldsymbol{b}\)所在的位置。那么,\(x_i\)就表示在这n个方向上,我分别走了多少步。
\[
\boldsymbol{A}\boldsymbol{x}=\sum _i x_i\boldsymbol{A}_{:,i}
\]
上面的式子表示,n个m维向量相加,得到一个m维向量这种操作称为线性组合(linear combination)。n个向量\({\boldsymbol{v}^{(1)},...,\boldsymbol{v}^{(n)}}\)的线性组合,指的就是每一个向量\(\boldsymbol{v}^{(i)}\)都乘以一个系数,并进行累加得到\(\sum _ic_i\boldsymbol{v}^{(i)}\)。
2.5 Norms
2.6 Special Kinds of Matrices and Vectors
2.7 Eigendecomposition
2.8 Singular Value Decomposition
2.9 The Moore-Penrose Pseudoinverse
2.10 The Trace Operator
2.11 The Determinant
2.12 Example: Principal Components Analysis
原创文章,转载请注明出处!
本文链接:http://daiwk.github.io/posts/dl-dlbook-chap2.html