目录

• 概述
• 引言
• 模型
  • 原始GNN
  • GNN变种
    • 图类型
      • Directed Graphs
      • Heterogeneous Graphs
      • Graphs with Edge Information
    • 传播类型(propagation types)
    • 训练方法
  • General Frameworks
    • Message Passing Neural Networks(MPNN)
    • Non-local Neural Networks(NLNN)
    • Graph Networks(GN)
• 应用
  • 结构化场景
  • 非结构化场景
  • 其他场景
• 开放性问题
• GNN的普适与局限性
• kdd 2019

概述

最近图神经网络有点火。。先mark一下：

清华大学孙茂松组：图神经网络必读论文列表

github链接：https://github.com/thunlp/GNNPapers

综述Graph Neural Networks: A Review of Methods and Applications

解读：图神经网络综述：模型与应用

又一篇综述：图神经网络概述第三弹：来自IEEE Fellow的GNN综述

又一个文献合集https://github.com/DeepGraphLearning/LiteratureDL4Graph

引言

图是一种数据结构，它对一组对象 （节点） 及其关系 （边） 进行建模。图神经网络（GNN）是一类基于深度学习的处理图域信息的方法。由于其较好的性能和可解释性，GNN 最近已成为一种广泛应用的图分析方法。

GNN的第一个动机源于卷积神经网络（CNN）：CNN只能在规则的Euclidean数据上运行，如图像（2维网格）和文本（1维序列）。如何将CNN应用于图结构这一非欧几里德空间，成为GNN模型重点解决的问题。

GNN的另一个动机来自图嵌入（Graph Embedding），它学习图中节点、边或子图的低维向量空间表示。DeepWalk、node2vec、LINE、SDNE等方法在网络表示学习领域取得了很大的成功。然而，这些方法在计算上较为复杂并且在大规模上的图上并不是最优的，GNN旨在解决这些问题。

模型

原始GNN

2009年的第一篇GNN的文章The graph neural network model。GNN的target是要学习包括了每个节点的邻居的信息的state embedding \(h_v\in R^s\)。这里的state embedding \(h_v\)是节点\(v\)的一个\(s\)维的向量，能用来产生输出\(o_v\)，例如节点的label。\(f\)是一个带有参数的函数，称为local transition function，被所有的节点共享，能根据输入的邻居来更新节点状态。\(g\)是local output function，表示如何产生output。所以：

\[ \begin{matrix} h_v=f(x_v,x_{co[v]},h_{ne[v]},x_{ne[v]})\\ o_v=g(h_v,x_v)\\ \end{matrix} \]

其中，

• \(x_v\)：节点\(v\)的特征。
• \(x_{co[v]}\)：节点\(v\)的边的特征。
• \(h_{ne[v]}\)：节点\(v\)的邻居节点的state。
• \(x_{ne[v]}\)：节点\(v\)的邻居节点的特征。

把所有状态、输出、特征、所有节点的特征stack到一起，就有了向量\(X\)、\(O\)、\(X\)和\(X_N\)。所以有：

\[ \begin{matrix} H=F(H,X)\\ O=G(H,X_N)\\ \end{matrix} \]

使用如下方式对状态进行迭代：

\[ H^{t+1}=F(H^t,X) \]

其中的\(f\)和\(g\)都可以用神经网络来表示。loss如下：

\[ loss=\sum ^p_{i=1}(t_i-o_i) \]

GNN变种

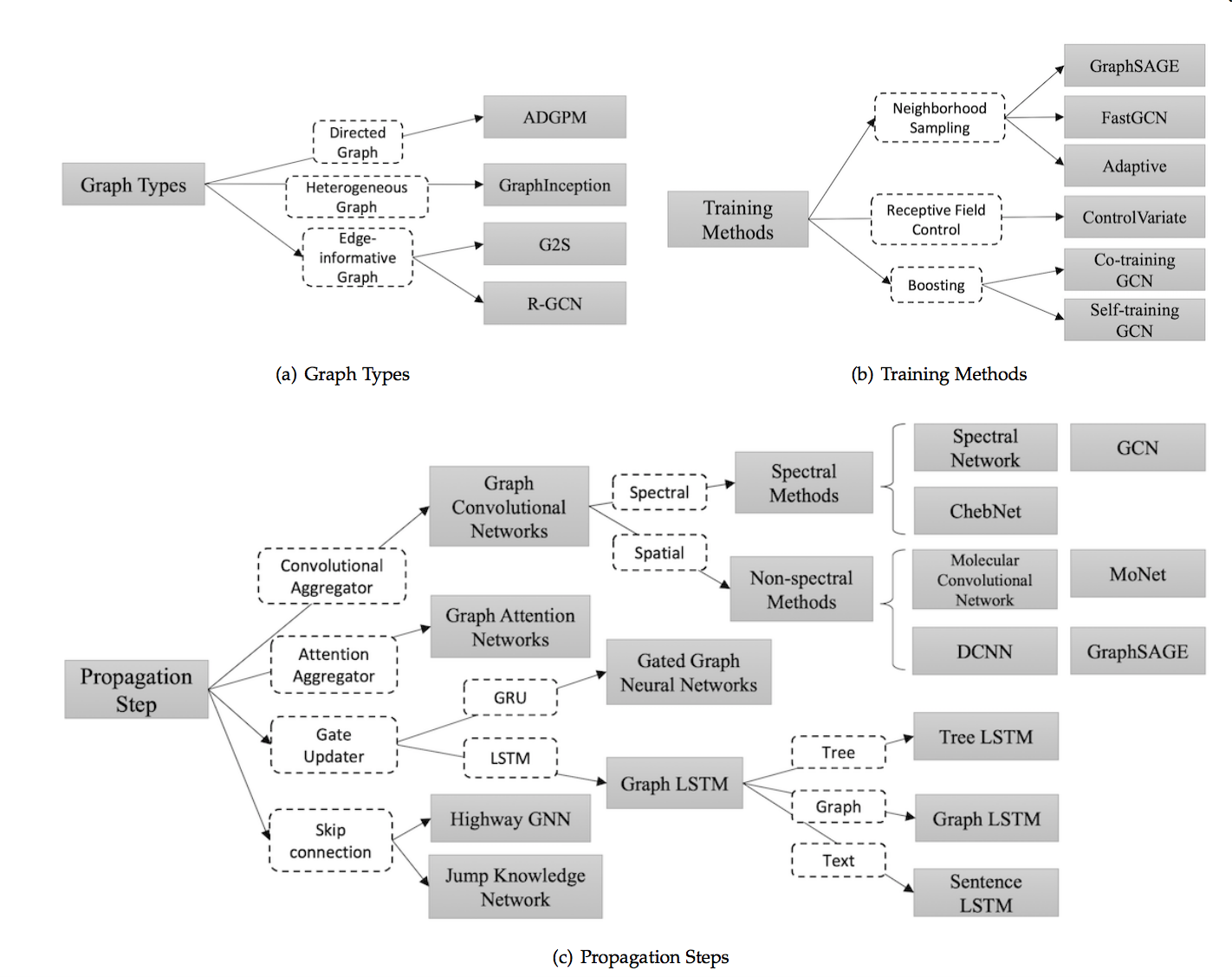
图类型

Directed Graphs

有向图。如图中的ADGPM【Rethinking knowledge graph propagation for zero-shot learning】，有两种权重矩阵\(W_p\)和\(W_c\)

\[H^t=\sigma(D^{-1}_pA_p\sigma(D^{-1}_cA_cH^{t-1}W_c)W_p)\]

其中的\(D^{-1}_pA_p\)和\(D^{-1}_cA_c\)分别是parent和children的normalized adjacency matrix。

Heterogeneous Graphs

异构图。如图中的GraphInception。

Graphs with Edge Information

边带有信息的图，如图中的G2S以及R-GCN。

传播类型(propagation types)

propagation step和output step这两部是很重要的，主要分为以下类别：

• 卷积：Graph Convolutional Network（GCN）希望将卷积操作应用在图结构数据上，主要分为Spectral Method和Spatial Method（Non-spectral Method）两类。
  • Spectral Method：希望使用谱分解的方法，应用图的拉普拉斯矩阵分解进行节点的信息收集。
  • Spatial Method：直接使用图的拓扑结构，根据图的邻居信息进行信息收集。
• 注意力机制：Graph Attention Network 致力于将注意力机制应用在图中的信息收集阶段。
• 门机制：门机制应用于节点更新阶段。Gated graph neural network 将GRU机制应用于节点更新。很多工作致力于将 LSTM应用于不同类型的图上，主要包括Tree LSTM、Graph LSTM和Sentence LSTM等
• 残差连接：堆叠多层图神经网络可能引起噪声在指数级增加的邻居中传播，所以很多工作将残差机制应用于图神经网络中。主要包括Highway GNN和Jump Knowledge Network两种不同的处理方式。

信息传递函数主要包括信息收集（agggregation）和节点信息更新（update）两个部分，公式见：

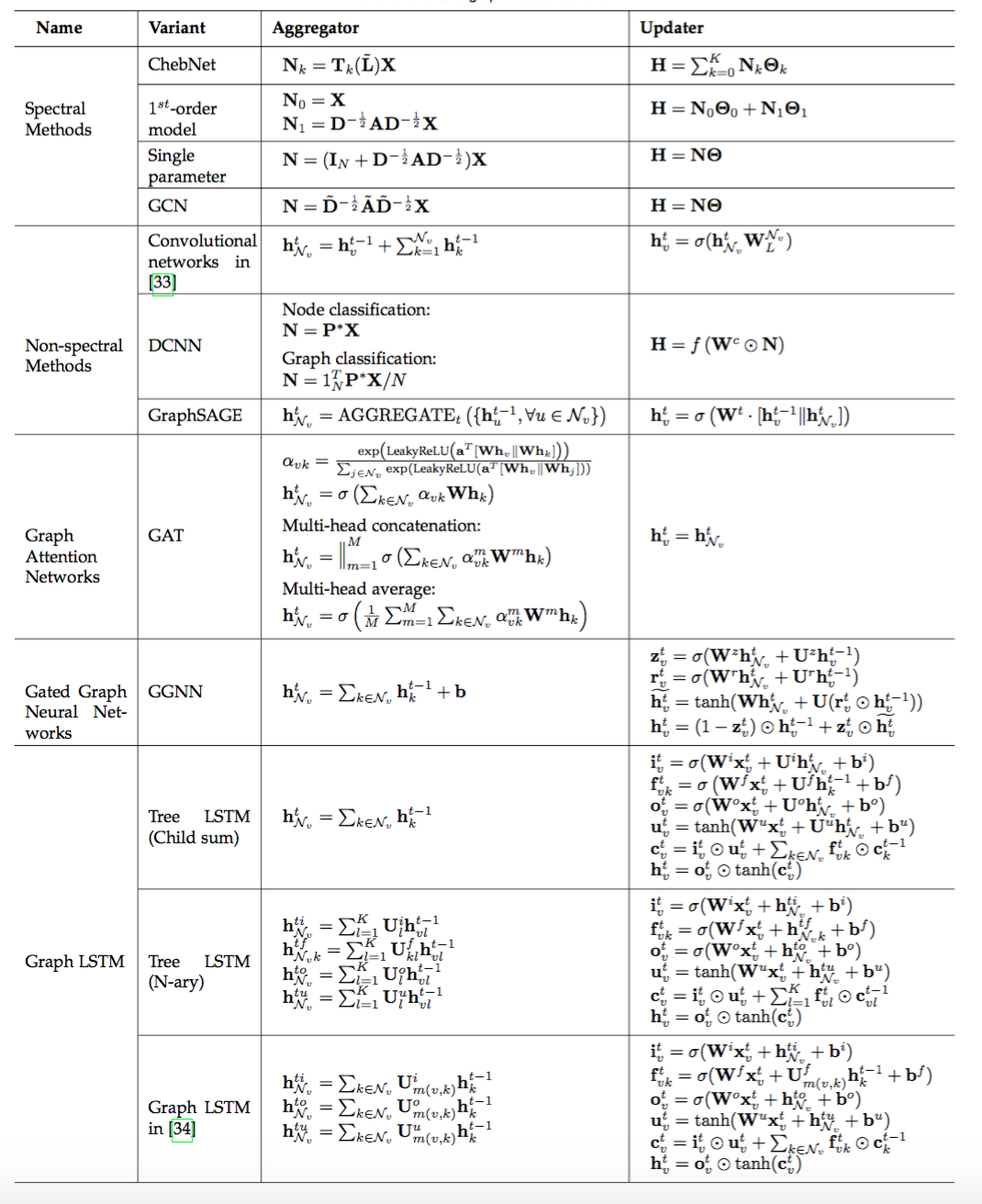
训练方法

譬如GraphSAGE从附近的邻居收集信息，并且能够应用于inductive learning领域；FastGCN使用了importance sampling的方法，使用采样替代使用节点所有的邻居信息，加快了训练过程。

General Frameworks

图神经网络通用框架主要包括MPNN（Message Passing Neural Network）、NLNN（Non-local Neural Network）以及 Deepmind 的 GN（Graph Network）。

Message Passing Neural Networks(MPNN)

MPNN将模型总结为信息传递阶段和节点更新阶段，概括了多种图神经网络和图卷积神经网络方法。

Non-local Neural Networks(NLNN)

NLNN总结了很多种基于自注意力机制的方法。

Graph Networks(GN)

GN提出了更加通用的模型，能够总结概括几乎所有文中提到的框架，并且拥有更加灵活的表示能力、易于配置的块内结构以及易于组合的多模块架构。

应用

应用见：

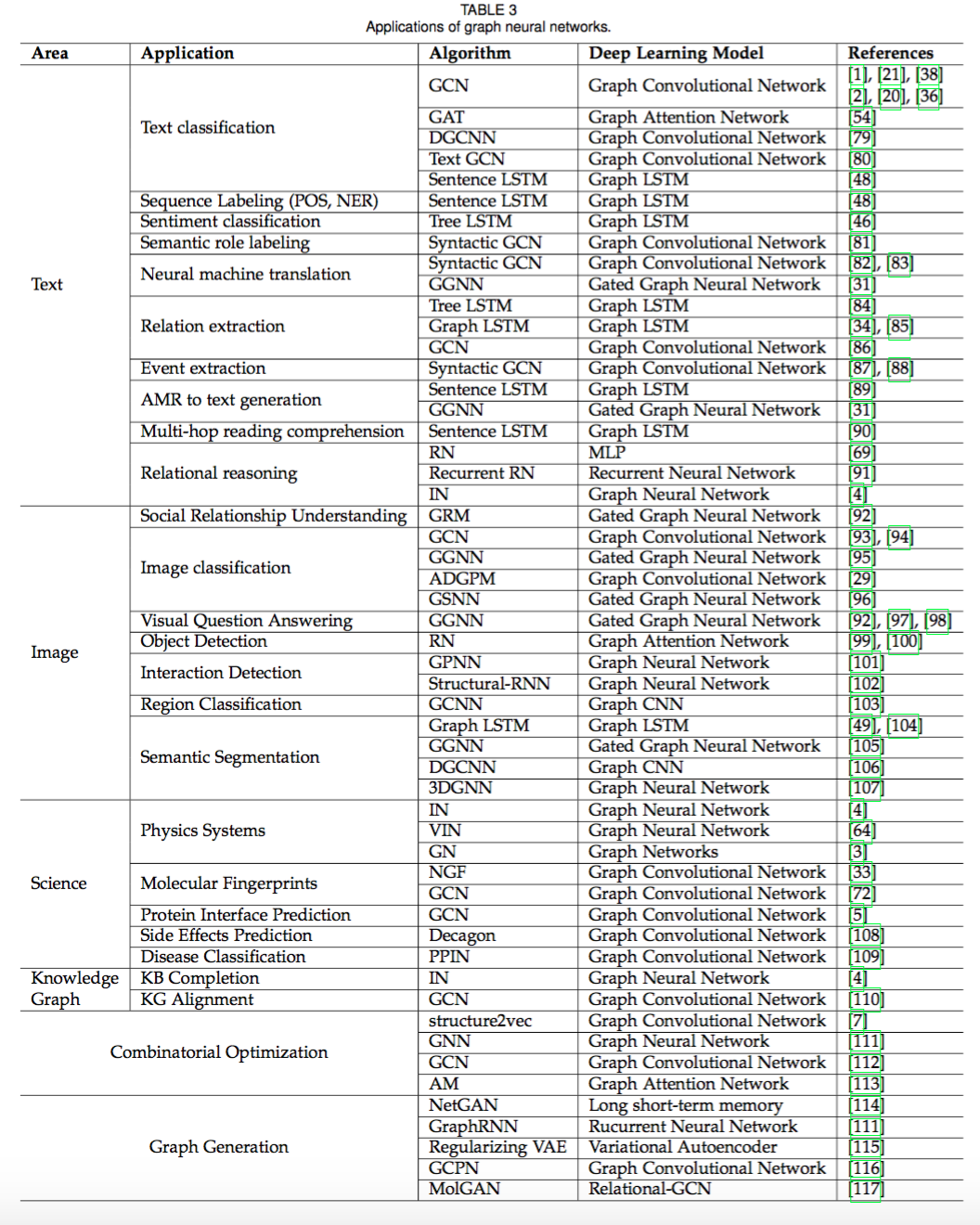
结构化场景

GNN 被广泛应用在社交网络、推荐系统、物理系统、化学分子预测、知识图谱等领域。

非结构化场景

在图像和文本中的应用

其他场景

图生成模型以及使用GNN来解决组合优化问题的场景。

开放性问题

1. 浅层结构。经验上使用更多参数的神经网络能够得到更好的实验效果，然而堆叠多层的GNN却会产生over-smoothing的问题。具体来说，堆叠层数越多，节点考虑的邻居个数也会越多，导致最终所有节点的表示会趋向于一致。
2. 动态图。目前大部分方法关注于在静态图上的处理，对于如何处理节点信息和边信息随着时间步动态变化的图仍是一个开放问题。
3. 非结构化场景。虽然很多工作应用于非结构化的场景（比如文本），然而并没有通用的方法用于处理非结构化的数据。
4. 扩展性。虽然已经有一些方法尝试解决这个问题，将图神经网络的方法应用于大规模数据上仍然是一个开放性问题。

GNN的普适与局限性

图神经网络火了？谈下它的普适性与局限性

kdd 2019

近期必读的12篇KDD 2019【图神经网络（GNN）】相关论文

上篇： drn