梯度下降优化算法
标签:梯度下降优化算法, momentum, NAG, Adagrad, Adadelta, RMSprop, Adam, Aadams, AMSGrad, Lookahead, RAdam, warm up目录
梯度下降
参考http://ruder.io/optimizing-gradient-descent/
部分算法有对应的中文版:https://blog.csdn.net/u010089444/article/details/76725843
优缺点参考:https://blog.csdn.net/u012759136/article/details/52302426
!!!假设模型的参数\(\theta \in \mathbb{R}^{d}\)
普通sgd有如下缺点:
- 选择合适的learning rate比较困难
- 对所有的参数更新使用同样的learning rate。对于稀疏数据或者特征,有时我们可能想更新快一些对于不经常出现的特征,对于常出现的特征更新慢一些,这时候SGD就不太能满足要求了
- SGD容易收敛到局部最优,在某些情况下可能被困在鞍点【但是在合适的初始化和学习率设置下,鞍点的影响其实没这么大】
momentum
如果在峡谷地区(某些方向较另一些方向上陡峭得多,常见于局部极值点),SGD会在这些地方附近振荡,从而导致收敛速度慢。这种情况下,动量(Momentum)便可以解决。动量在参数更新项中加上一次更新量(即动量项)。
\[
\begin{aligned} v_{t} &=\gamma v_{t-1}+\eta \nabla_{\theta} J(\theta) \\ \theta &=\theta-v_{t} \end{aligned}
\]
其中,\(\eta\)一开始初始化为0.5,后面变成0.9。一般直接设成0.9好了。。http://ufldl.stanford.edu/tutorial/supervised/OptimizationStochasticGradientDescent/
简单地说,就是记录每次的权重更新量,这次的更新量就是上次更新量乘上一个系数,再加上学习率乘以梯度。
特点:
- 下降初期,使用上一次参数更新,下降方向一致,乘上较大的
\(\gamma\)能够进行很好的加速 - 下降中后期时,在局部最小值来回震荡的时候,梯度接近0,
\(\gamma\)使得更新幅度变大,可能可以跳出陷阱 - 梯度改变方向的时候,
\(\gamma\)可以减少更新
NAG
Nesterov accelerated gradient (NAG)
\[
\begin{aligned} v_{t} &=\gamma v_{t-1}+\eta \nabla_{\theta} J\left(\theta-\gamma v_{t-1}\right) \\ \theta &=\theta-v_{t} \end{aligned}
\]
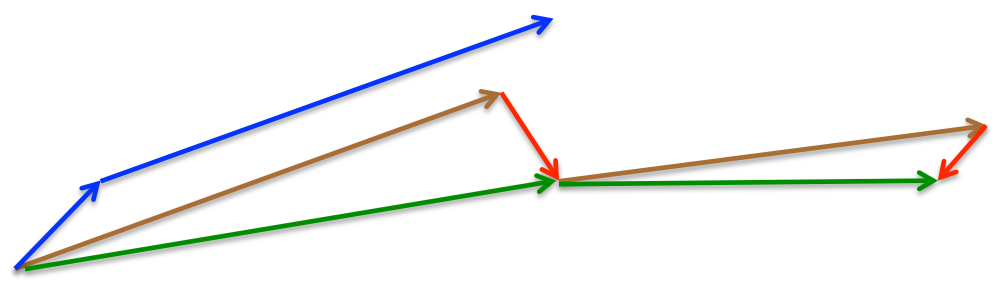
momentum首先计算一个梯度(短的蓝色向量),然后在加速更新梯度的方向进行一个大的跳跃(长的蓝色向量),nesterov项首先在之前加速的梯度方向进行一个大的跳跃(棕色向量),计算梯度然后进行校正(绿色梯向量)
Adagrad
首先
\[
g_{t, i}=\nabla_{\theta} J\left(\theta_{t, i}\right)
\]
然后
\[
\theta_{t+1, i}=\theta_{t, i}-\eta \cdot g_{t, i}
\]
再然后
\[
\theta_{t+1, i}=\theta_{t, i}-\frac{\eta}{\sqrt{G_{t, i i}+\epsilon}} \cdot g_{t, i}
\]
其中,\(G_{t} \in \mathbb{R}^{d \times d}\)是一个对角矩阵,每个对角线位置\(i,i\)为对应参数\(\theta_i\)从第1轮到第t轮梯度的平方和。
综合起来看就是
\[
\theta_{t+1}=\theta_{t}-\frac{\eta}{\sqrt{G_{t}+\epsilon}} \odot g_{t}
\]
也就是学习率除以前t轮的梯度的平方和加上一个\(\epsilon\)再开根号。这个\(\epsilon\)一般设置成\(1 e-8\)。
特点:
- 前期梯度小时,分母大,能放大梯度
- 后期梯度大时,分母小,能约束梯度
- 适合处理稀疏梯度
缺点:
- 仍然依赖人为设置的全局学习率
- 学习率设置得太大的话,会使得对梯度的调节太大
- 中后期,分母会越来越大,梯度趋近0,训练会提前结束
Adadelta
有点长。。
首先
\[
E\left[g^{2}\right]_{t}=\gamma E\left[g^{2}\right]_{t-1}+(1-\gamma) g_{t}^{2}
\]
然后
\[
\begin{array}{l}{\Delta \theta_{t}=-\eta \cdot g_{t, i}} \\ {\theta_{t+1}=\theta_{t}+\Delta \theta_{t}}\end{array}
\]
再然后,adagrad是这样的:
\[
\Delta \theta_{t}=-\frac{\eta}{\sqrt{G_{t}+\epsilon}} \odot g_{t}
\]
而我们把那个平方和替换成平均:
\[
\Delta \theta_{t}=-\frac{\eta}{\sqrt{E\left[g^{2}\right]_{t}+\epsilon}} g_{t}
\]
其实就是RMS(root mean square),也就是\(R M S[g]_{t}=\sqrt{E\left[g^{2}\right]_{t}+\epsilon}\),代入上式可以得到:
\[
\Delta \theta_{t}=-\frac{\eta}{R M S[g]_{t}} g_{t}
\]
然后呢,定义一个参数平方的更新量\(\Delta \theta _t^2\)的指数平滑:
\[
E\left[\Delta \theta^{2}\right]_{t}=\gamma E\left[\Delta \theta^{2}\right]_{t-1}+(1-\gamma) \Delta \theta_{t}^{2}
\]
然后参数更新量\(\Delta \theta _t\)的RMSE就是:
\[
R M S[\Delta \theta]_{t}=\sqrt{E\left[\Delta \theta^{2}\right]_{t}+\epsilon}
\]
而\(R M S[\Delta \theta]_{t}\)是未知的,可以用直到上一个时间步的参数更新的RMS来近似。所以可以拿\(R M S[\Delta \theta]_{t-1}\)来替换学习率\(\eta\),从而得到:
\[
\begin{aligned} \Delta \theta_{t} &=-\frac{R M S[\Delta \theta]_{t-1}}{R M S[g]_{t}} g_{t} \\ \theta_{t+1} &=\theta_{t}+\Delta \theta_{t} \end{aligned}
\]
特点:
- 已经不用依赖于全局学习率了
- 训练初中期,加速效果不错,很快
- 训练后期,反复在局部最小值附近抖动
RMSprop
\[
\begin{aligned} E\left[g^{2}\right]_{t} &=0.9 E\left[g^{2}\right]_{t-1}+0.1 g_{t}^{2} \\ \theta_{t+1} &=\theta_{t}-\frac{\eta}{\sqrt{E\left[g^{2}\right]_{t}+\epsilon}} g_{t} \end{aligned}
\]
就是在adagrad的基础上,分母那个平方和改成指数平滑,前一时间步0.9,当前时间步0.1,而且前一时间步依赖的是均值而不是平方和,与adadelta类似。hinton认为\(\gamma\)设成0.9,默认学习率\(\eta\)设0.01比较好。
特点:
- 依赖于全局学习率
- RMSprop算是Adagrad的一种发展,和Adadelta的变体,效果趋于二者之间
- 适合处理非平稳目标
- 对于RNN效果很好
Adam
rmsprop可以看成是对二阶矩做了指数平滑,adam就是对一阶矩也做一个指数平滑。然后二阶和一阶平滑完后要scale一下。最后二阶的搞完做分母,一阶的搞完做分子。
两个的指数平滑如下:
\[
\begin{aligned} m_{t} &=\beta_{1} m_{t-1}+\left(1-\beta_{1}\right) g_{t} \\ v_{t} &=\beta_{2} v_{t-1}+\left(1-\beta_{2}\right) g_{t}^{2} \end{aligned}
\]
然后:
\[
\begin{aligned} \hat{m}_{t} &=\frac{m_{t}}{1-\beta_{1}^{t}} \\ \hat{v}_{t} &=\frac{v_{t}}{1-\beta_{2}^{t}} \end{aligned}
\]
再然后:
\[
\theta_{t+1}=\theta_{t}-\frac{\eta}{\sqrt{\hat{v}_{t}}+\epsilon} \hat{m}_{t}
\]
默认值的话,\(\beta_1=0.9\),\(\beta_2=0.999\),\(\epsilon=10^{-8}\)
特点:
- 结合了Adagrad善于处理稀疏梯度和RMSprop善于处理非平稳目标的优点
- 对内存需求较小
- 为不同的参数计算不同的自适应学习率
- 也适用于大多非凸优化
- 适用于大数据集和高维空间
Adam类方法小结
参考https://blog.csdn.net/wishchin/article/details/80567558
结论:
- Adam算法可以看做是修正后的Momentum+RMSProp算法
- 动量直接并入梯度一阶矩估计中(指数加权)
- Adam通常被认为对超参数的选择相当鲁棒
- 学习率建议为0.001
其实就是Momentum+RMSProp的结合,然后再修正其偏差。
AMSGrad
Adams其实有不少问题,参考https://zhuanlan.zhihu.com/p/32262540
论文:On the Convergence of Adam and Beyond
参考https://blog.csdn.net/wishchin/article/details/80567558
\[
\Gamma_{t+1}=\left(\frac{\sqrt{V_{t+1}}}{\alpha_{t+1}}-\frac{\sqrt{V_{t}}}{\alpha_{t}}\right)
\]
RMSProp和Adam算法下的\(\Gamma_{t}\)可能是负的,所以文章探讨了一种替代方法,通过把超参数\(\beta_1\)、\(\beta_2\)设置为随着\(t\)变化而变化,从而保证\(\Gamma_{t}\)始终是个非负数。
Lookahead
论文:Lookahead Optimizer: k steps forward, 1 step back
参考Adam作者大革新, 联合Hinton等人推出全新优化方法Lookahead
dlADMM
KDD 2019 | 不用反向传播就能训练DL模型,ADMM效果可超梯度下降
ADMM for Efficient Deep Learning with Global Convergence
代码:https://github.com/xianggebenben/dlADMM
本文提出了一种基于交替方向乘子法的深度学习优化算法 dlADMM。该方法可以避免随机梯度下降算法的梯度消失和病态条件等问题,弥补了此前工作的不足。此外,该研究提出了先后向再前向的迭代次序加快了算法的收敛速度,并且对于大部分子问题采用二次近似的方式进行求解,避免了矩阵求逆的耗时操作。在基准数据集的实验结果表明,dlADMM 击败了大部分现有的优化算法,进一步证明了它的有效性和高效。
RAdam
Adam可以换了?UIUC中国博士生提出RAdam,收敛快精度高,大小模型通吃
github: https://github.com/LiyuanLucasLiu/RAdam
On the variance of the adaptive learning rate and beyond
它既能实现Adam快速收敛的优点,又具备SGD方法的优势,令模型收敛至质量更高的结果。
包括Adam,RMSProp等在内的自适应学习率优化器都存在收敛到质量较差的局部最优解的可能。因此,几乎每个人都使用某种形式的“预热”方式来避免这种风险。
根本问题是自适应学习率优化器具有太大的变化,特别是在训练的早期阶段,并且可能由于训练数据量有限出现过度跳跃,因此可能收敛至局部最优解。
当优化器仅使用有限的训练数据时,采用“预热”(这一阶段的学习率要慢得多)是自适应优化器要求抵消过度方差的要求。
vanilla Adam和其他自适应学习速率优化器可能会基于训练早期数据太少而做出错误决策。因此,如果没有某种形式的预热,很可能在训练一开始便会收敛局部最优解,这使得训练曲线由于糟糕的开局而变得更长、更难。
作者在不用预热的情况下运行了Adam,但是在前2000次迭代(adam-2k)中避免使用动量,结果实现了与“Adam+预热”差不多的结果,从而验证了“预热”在训练的初始阶段中起到“降低方差”的作用,并可以避免Adam在没有足够数据的情况下在开始训练时即陷入局部最优解。
可以将“预热”作为降低方差的方法,但所需的预热程度未知,而且具体情况会根据数据集不同而变化,本文确定了一个数学算法,作为“动态方差减少器”。作者建立了一个“整流项”,可以缓慢而稳定地允许将自适应动量作为基础方差的函数进行充分表达。
作者指出,在某些情况下,由于衰减率和基本方差的存在,RAdam可以在动量等效的情况下退化为SGD。
实验表明,RAdam优于传统的手动预热调整,其中需要预热或猜测需要预热的步骤数。RAdam自动提供方差缩减,在各种预热长度和各种学习率下都优于手动预热。
warm-up
Deep Residual Learning for Image Recognition中对cifar10的实验用了一个trick是 warm up(热身),就是先采用小的学习率(0.01)进行训练,训练了400iterations之后将学习率调整至0.1开始正式训练。
参考知乎的这个问题:https://www.zhihu.com/question/338066667
- 有助于减缓模型在初始阶段对mini-batch的提前过拟合现象,保持分布的平稳
- 有助于保持模型深层的稳定性
可以参考这几篇:
原创文章,转载请注明出处!
本文链接:http://daiwk.github.io/posts/dl-optimization-methods.html