目录

• EM算法

EM算法

参考https://blog.csdn.net/fuqiuai/article/details/79484421

分布式的EM，以PLSI为例，看google www07发的那篇讲google news的推荐算法的：Google News Personalization: Scalable Online Collaborative Filtering

对于\(T\)个训练样本来讲，新闻是\(s\)，用户是\(u\)，引入一个中间隐变量\(z\)，就有两个条件概率(CPD, conditional probability distribution)\(p(z|u)\)和\(p(s|z)\)，(也就是从u到z再到s)然后就是要最大化条件似然的乘积，也就是要最小化负的经验log风险：

\[ L(\theta) = - \frac{1}{T}\sum ^{T}_{t=1}\log(p(s_t|u_t;\theta)) \]

而这可以通过EM来解。

E-step计算如下的\(Q\)值，也就是后验的隐变量的概率：

\[ q^*(z;u,s;\hat{\theta}):=p(z|u,s;\hat{\theta})=\frac{\hat{p}(s|z)\hat{p}(z|u)}{\sum_{z\in Z}\hat{p}(s|z)\hat{p}(z|u)} \]

M-step使用上面的Q计算如下分布：

\[ \begin{matrix} p(s|z) &= \frac{\sum_uq^*(z;u,s;\hat{\theta})}{\sum_s\sum_uq^*(z;u,s;\hat{\theta})}\\ p(z|u) &= \frac{\sum_sq^*(z;u,s;\hat{\theta})}{\sum_z\sum_sq^*(z;u,s;\hat{\theta})} \end{matrix} \]

其中的\(\hat{p}\)指的是上一轮EM迭代产出的\(p\)。

假设M=N=1kw，L=1000,也就是1kw个user，1kw个item，然后有1000个隐变量，那么需要存\((M+N)\times L\times 4=80GB\)的内存来存储两个CPD(假设double占4字节)。单机是不行的，搞成分布式的。。

加两个中间项：

\[ \begin{matrix} N(z,s)=\sum_uq^*(z;u,s;\hat{\theta})\\ N(z)=\sum_s\sum_u^*(z;u,s;\hat{\theta}) \end{matrix} \]

那么，

\[ q^*(z;u,s;\hat{\theta}):=p(z|u,s;\hat{\theta})=\frac{\frac{N(z,s)}{N(z)}\hat{p}(z|u)}{\sum_{z\in Z}\frac{N(z,s)}{N(z)}\hat{p}(z|u)} \]

其中，

\[ \hat{p}(z|u) = \frac{\sum_sq^*(z;u,s;\hat{\theta})}{\sum_z\sum_sq^*(z;u,s;\hat{\theta})} \]

这样，就可以把\(p(s|z)\)干掉了

对于每个给定的(u,s)的pair对，计算 \(q^*(z;u,s;\hat{\theta}):=p(z|u,s;\hat{\theta})\)时，需要之前多轮迭代的信息：\(\hat{p}(z|u)\)、\(N(z,s)\)和\(N(z)\)。当统计信息足够多时，对于一个(u,s)对，计算\(q^*\)是可以独立且并行的。

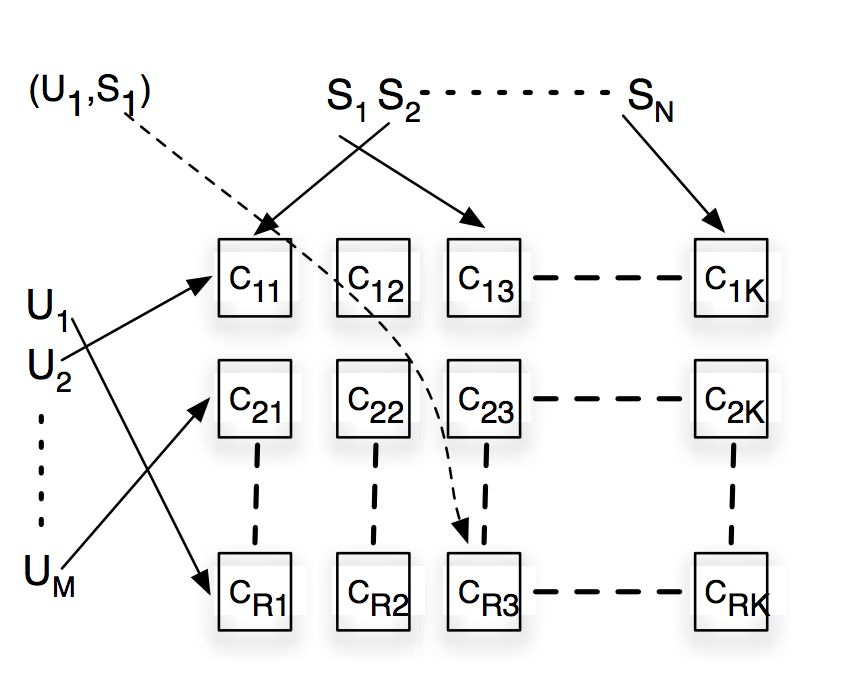
我们看一个\(R\times K\)的shard。假设所有用户被hash到\(R\)个group里，所有news被hash到\(K\)个group里。也就是说\((u_1,s_1)\)这个pair对，按下图就是被分到了\(C_{R3}\)这个shard里去了。然后在一个shard中，只要存储这个shard里的所有(u,s)的pair对的点展信息就行了，来计算里面的CPD。所以一个shard需要存的CPD就只有1/R的用户的CPD和1/K的news的CPD。

map输出3个kv：\((u,q^*)\)、\((i,q^*)\)和\((z,q^*)\)。

对于reduce来说，

• 负责s的reduce对所有的z计算\(N(z,s)\)
• 负责u的reduce计算\(p(z|u)\)
• 负责z的reduce计算\(N(z)\)。每一个(u,s)的pair就会产出一条记录给负责z的reduce。。所以可以在shuffle阶段做一些预处理，防止reduce单节点太慢