word2vec
标签:word2vec, ngram, nnlm, cbow, c-skip-gram, 统计语言模型目录
- 1. 统计语言模型
- 2. CBOW(Continuous Bag-of-Words)
- 3. Continuous skip-gram
- 4. HS & NCE
- 5. 面试常见问题
- x. tensorflow的简单实现
- y1. tensorflow的高级实现1
- y2. tensorflow的高级实现2
- 自己的总结
参考cdsn博客:http://blog.csdn.net/zhaoxinfan/article/details/27352659
参考paddlepaddle book: https://github.com/PaddlePaddle/book/blob/develop/04.word2vec/README.cn.md
参考fasttext及更多cbow/skip-gram:https://daiwk.github.io/posts/nlp-fasttext.html
Word2vec的原理主要涉及到统计语言模型(包括N-gram模型和神经网络语言模型(nnlm)),continuous bag-of-words模型以及continuous skip-gram模型。
语言模型旨在为语句的联合概率函数\(P(w_1,...,w_T)\)建模。语言模型的目标是,希望模型对有意义的句子赋予大概率,对没意义的句子赋予小概率。 常用条件概率表示语言模型:
\[
P(w_1, ..., w_T) = \prod_{t=1}^TP(w_t | w_1, ... , w_{t-1})
\]
1. 统计语言模型
N-gram模型
n-gram是一种重要的文本表示方法,表示一个文本中连续的n个项。基于具体的应用场景,每一项可以是一个字母、单词或者音节。一般用每个n-gram的历史n-1个词语组成的内容来预测第n个词。
神经网络语言模型(NNLM)
Yoshua Bengio等科学家就于2003年在著名论文 Neural Probabilistic Language Models中介绍如何学习一个神经元网络表示的词向量模型。神经概率语言模型(Neural Network Language Model,NNLM)通过一个线性映射和一个非线性隐层连接,同时学习了语言模型和词向量,即通过学习大量语料得到词语的向量表达,通过这些向量得到整个句子的概率。用这种方法学习语言模型可以克服维度灾难(curse of dimensionality),即训练和测试数据不同导致的模型不准。
实际上越远的词语其实对该词的影响越小,那么如果考虑一个n-gram, 每个词都只受其前面n-1个词的影响,则有:
\[
P(w_1, ..., w_T) = \prod_{t=n}^TP(w_t|w_{t-1}, w_{t-2}, ..., w_{t-n+1})
\]
给定一些真实语料,这些语料中都是有意义的句子,N-gram模型的优化目标则是最大化目标函数:
\[
\frac{1}{T}\sum_t f(w_t, w_{t-1}, ..., w_{t-n+1};\theta) + R(\theta)
\]
其中,\(f(w_t, w_{t-1}, ..., w_{t-n+1})\)表示根据历史n-1个词得到当前词\(w_t\)的条件概率,\(R(\theta)\)表示参数正则项。
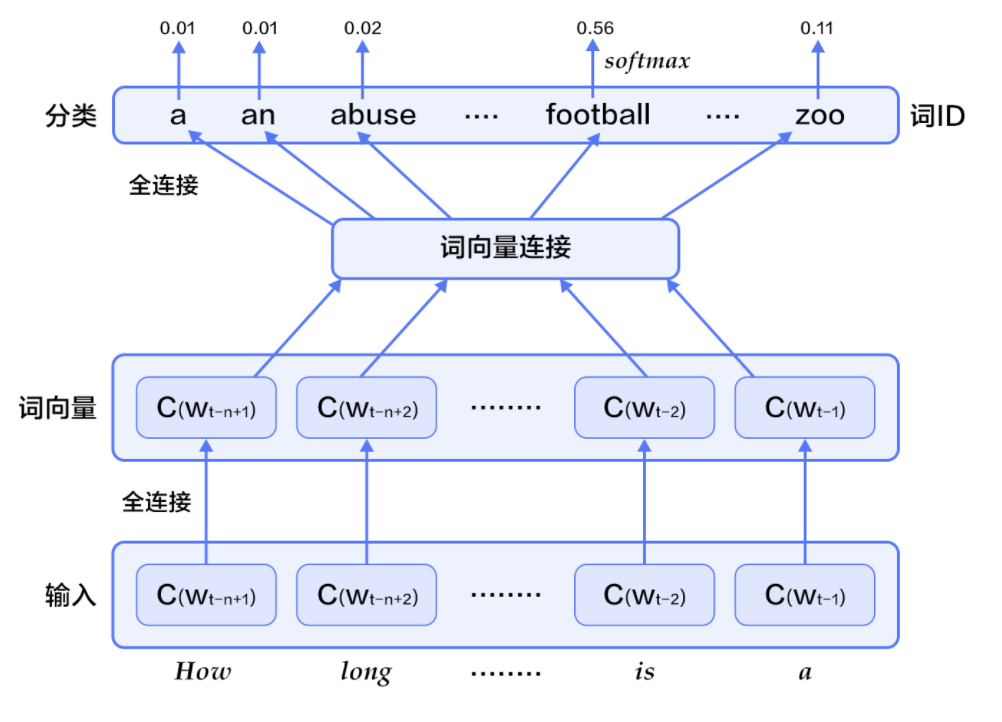
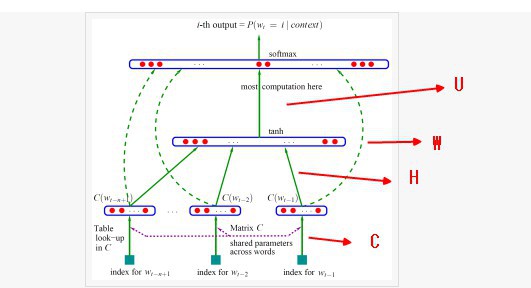
-
对于每个样本,模型输入
\(w_{t-n+1},...w_{t-1}\),输出句子第t个词为字典中\(|V|\)个词的概率。每个输入词\(w_{t-n+1},...w_{t-1}\)通过矩阵\(C\)映射到词向量\(C(w_{t-n+1}),...C(w_{t-1})\) -
然后所有词语的词向量连接成一个大向量,并经过一个非线性映射得到历史词语的隐层表示:
\[
g=Utanh(\theta^Tx + b_1) + Wx + b_2
\]
其中,x为所有词语的词向量连接成的大向量,表示文本历史特征;\(g\)表示未经归一化的所有输出单词概率,\(g_i\)表示未经归一化的字典中第i个单词的输出概率。其他参数为词向量层到隐层连接的参数。
- 根据softmax的定义,通过归一化
\(g_i\), 生成目标词\(w_t\)的概率为:
\[
P(w_t | w_1, ..., w_{t-n+1}) = \frac{e^{g_{w_t}}}{\sum_i^{|V|} e^{g_i}}
\]
- 整个网络的损失值(cost)为多类分类交叉熵,用公式表示为:
\[
J(\theta) = -\sum_{i=1}^N\sum_{c=1}^{|V|}y_k^{i}log(softmax(g_k^i))
\]
其中\(y_k^i\)表示第i个样本第k类的真实标签(0或1),\(softmax(g_k^i)\)表示第i个样本第k类softmax输出的概率。
2. CBOW(Continuous Bag-of-Words)
CBOW模型通过一个词的上下文(各N个词)预测当前词。当N=2时,模型如下图所示:
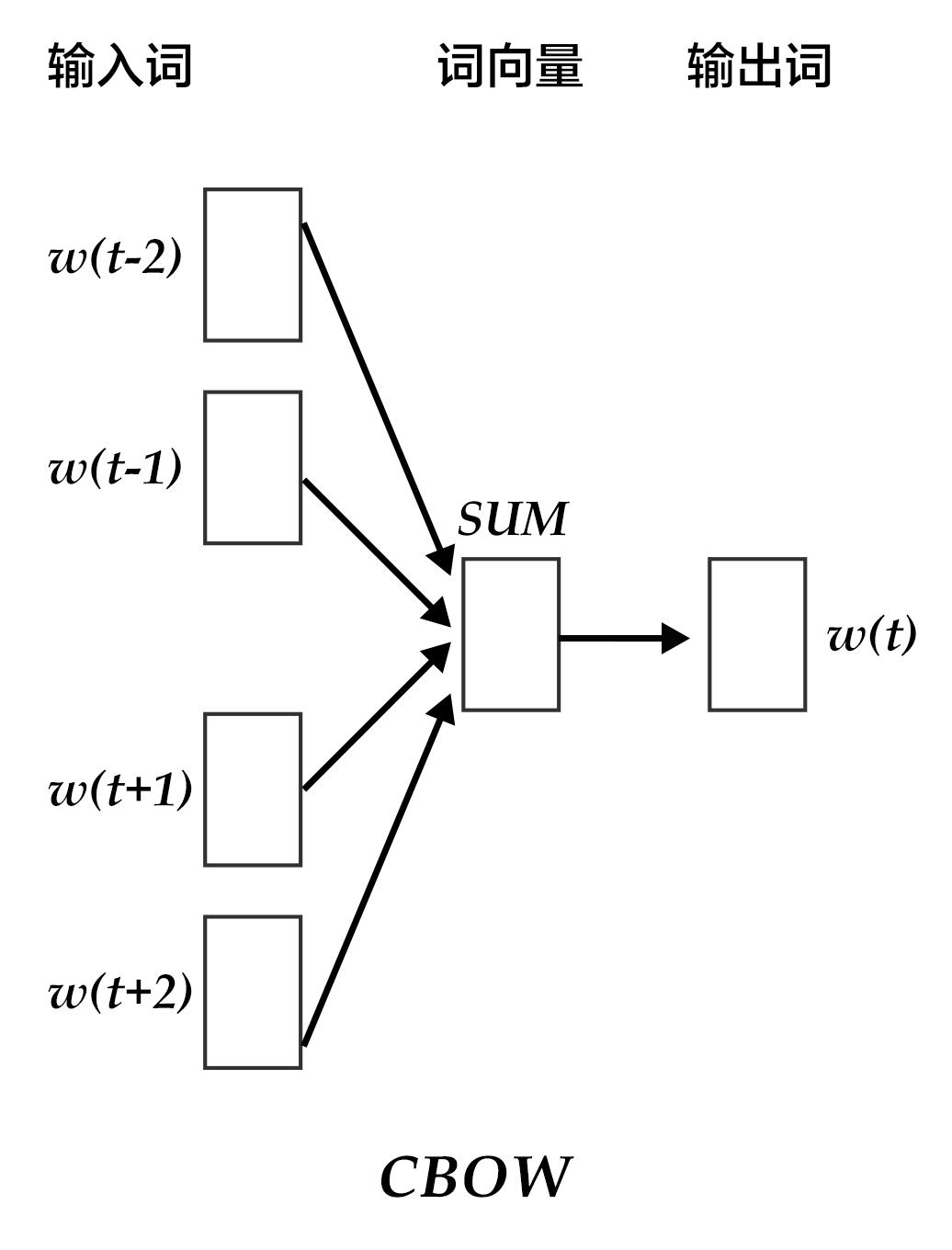
具体来说,不考虑上下文的词语输入顺序,CBOW是用上下文词语的词向量的均值来预测当前词。即:
\[
context = \frac{x_{t-1} + x_{t-2} + x_{t+1} + x_{t+2}}{4}
\]
其中\(x_t\)为第t个词的词向量,分类分数(score)向量 \(z=U*context\),最终的分类y采用softmax,损失函数采用多类分类交叉熵。
CBOW经常结合hierarchical softmax一起实现,详见https://daiwk.github.io/posts/nlp-fasttext.html#02-%E5%88%86%E5%B1%82softmax
3. Continuous skip-gram
CBOW的好处是对上下文词语的分布在词向量上进行了平滑,去掉了噪声,因此在小数据集上很有效。而Skip-gram的方法中,用一个词预测其上下文,得到了当前词上下文的很多样本,因此可用于更大的数据集。
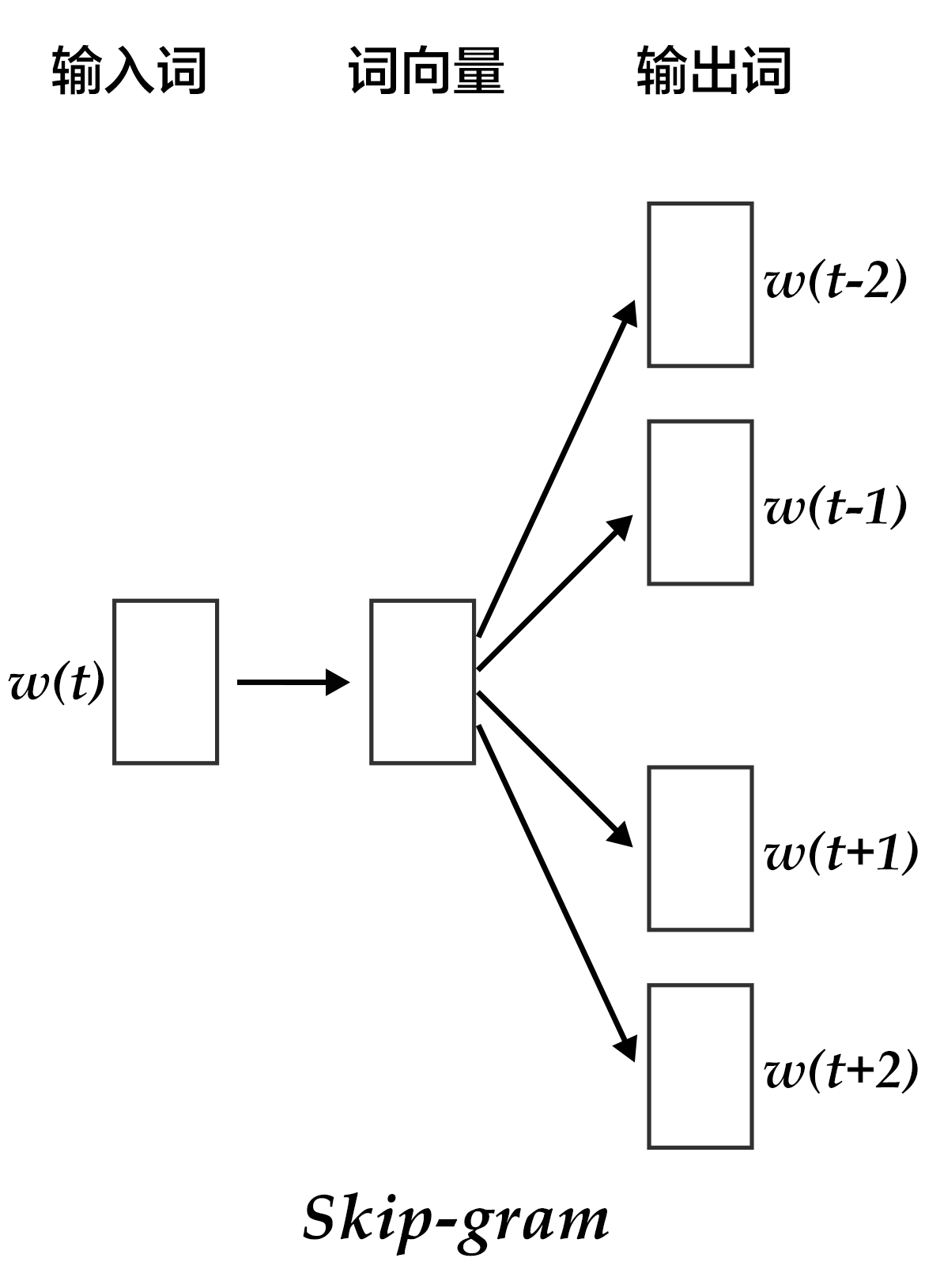
如上图所示,Skip-gram模型的具体做法是,将一个词的词向量映射到2n个词的词向量(2n表示当前输入词的前后各n个词),然后分别通过softmax得到这2n个词的分类损失值之和。
参考https://blog.csdn.net/u014595019/article/details/54093161
『我当时使用的是Hierarchical Softmax+CBOW的模型。给我的感觉是比较累,既要费力去写huffman树,还要自己写计算梯度的代码,完了按层softmax速度还慢。这次我决定用tensorflow来写,除了极大的精简了代码以外,可以使用gpu对运算进行加速。此外,这次使用了负采样(negative sampling)+skip-gram模型,从而避免了使用Huffman树导致训练速度变慢的情况,适合大规模的文本。』
而且,在tf中的实现tensorflow/tensorflow/examples/tutorials/word2vec/word2vec_basic.py,也是基于skip-gram+nce_loss的。
4. HS & NCE
word2vec的主要改进有两点:
- 对于从输入层到隐藏层的映射,没有采取神经网络的线性变换加激活函数,而是直接简单地对所有输入词向量求和并取平均
- 从隐藏层到输出的softmax层这里的计算量进行改进。而这个改进主要有hierarchical softmax和nce两种方式
4.1 hierachical softmax
参考http://www.cnblogs.com/pinard/p/7243513.html
所谓哈夫曼树,就是一个二叉树,每个叶子节点和中间节点都有权重(不是边有权重)。比如有\(V\)个词,那就是有\(V\)个叶子节点,每个节点的权重一般是词频。把这\(V\)个节点从大到小排序,第一次迭代是找到最小的两个叶子节点,生成他们的一个新的根节点(权重为两个叶子权重之和),完成一次迭代。第二次迭代就是这个根和其他叶子里,找出最小的两个,再生成一个根,如此继续。迭代的过程中要保证权重大的在左边,权重小的在右边。
在w2v中,我们规定向左走,就是负类(哈夫曼编码1)\(P(-)\),向右走就是正类(哈夫曼编码0)\(P(+)\)。判别正负类根据sigmoid:
\[
\begin{align*}
P(+) &= \sigma(x_w^T\theta) = \frac{1}{1+e^{-x_w^T\theta}} \\
P(-) &= 1-P(+) \\
\end{align*}
\]
其中,\(x_w\)是当前内部节点的词向量,\(\theta\)是当前节点的模型参数。
在某一个内部节点,要判断是沿左子树还是右子树走的标准就是看\(P(−)\)和\(P(+)\)谁的概率值大。
我们的目标就是找到合适的所有节点的词向量和所有内部节点\(\theta\), 使训练样本达到最大似然。
哈夫曼树主要有两个好处:
- 计算量由
\(V\)变为\(log_2V\) - 高频的词靠近树根,这样高频词需要更少的时间会被找到
Hierarchical Softmax梯度计算
假设我们要的一个叶子是通过『左、左、右』三步得到的,那么我们期望最大化如下的似然函数:
\[
\prod_{i=1}^3P(n(w_i),i) = (1- \frac{1}{1+e^{-x_w^T\theta_1}})(1- \frac{1}{1+e^{-x_w^T\theta_2}})\frac{1}{1+e^{-x_w^T\theta_3}}
\]
假设
\(w\):输入的词\(x_w\):输入的词从输入层词向量求和平均后的霍夫曼树根节点词向量\(l_w\):从根节点到\(w\)所在的叶子节点的路径上包含的节点总数\(p^w_i\):从根节点开始,经过的第i个节点,\(i = 2,3,...,l_w\)\(d^w_i\in {0,1}\):从根节点开始,经过的第i个节点的哈夫曼编码,\(i = 2,3,...,l_w\)\(\theta ^w_i\):从根节点开始,经过的第i个中间节点的模型参数,因为是中间节点,所以\(i = 1,2,...,l_w-1\)
在走到目标词\(w\)的路上经过的某个节点\(j\)的概率:
\[
P(d_j^w|x_w, \theta_{j-1}^w)= \begin{cases} \sigma(x_w^T\theta_{j-1}^w)& {d_j^w=0}\\ 1- \sigma(x_w^T\theta_{j-1}^w) & {d_j^w = 1} \end{cases}
\]
所以对于某个目标输出的叶子节点\(w\),最大似然是整条路径的概率连乘:
\[
\prod_{j=2}^{l_w}P(d_j^w|x_w, \theta_{j-1}^w) = \prod_{j=2}^{l_w} [\sigma(x_w^T\theta_{j-1}^w)] ^{1-d_j^w}[1-\sigma(x_w^T\theta_{j-1}^w)]^{d_j^w}
\]
所以其对数似然就是:
\[
L= log \prod_{j=2}^{l_w}P(d_j^w|x_w, \theta_{j-1}^w) = \sum\limits_{j=2}^{l_w} ((1-d_j^w) log [\sigma(x_w^T\theta_{j-1}^w)] + d_j^w log[1-\sigma(x_w^T\theta_{j-1}^w)])
\]
求参数\(\theta_{j-1}^w\)的梯度:
\[
\begin{align*}
\frac{\partial L}{\partial \theta_{j-1}^w} & = (1-d_j^w)\frac{\sigma(x_w^T\theta_{j-1}^w)(1-\sigma(x_w^T\theta_{j-1}^w))}{\sigma(x_w^T\theta_{j-1}^w)}x_w - d_j^w \frac{\sigma(x_w^T\theta_{j-1}^w)(1-\sigma(x_w^T\theta_{j-1}^w))}{1- \sigma(x_w^T\theta_{j-1}^w)}x_w \\
& = (1-d_j^w)(1-\sigma(x_w^T\theta_{j-1}^w))x_w - d_j^w\sigma(x_w^T\theta_{j-1}^w)x_w \\
& = (1-d_j^w-\sigma(x_w^T\theta_{j-1}^w))x_w
\end{align*}
\]
同样地,对参数\(x_w\)的梯度是:
\[
\frac{\partial L}{\partial x_w} = \sum\limits_{j=2}^{l_w}(1-d_j^w-\sigma(x_w^T\theta_{j-1}^w))\theta_{j-1}^w
\]
可以发现,都有\((1-d_j^w-\sigma(x_w^T\theta_{j-1}^w))\)这一项,只是对\(\theta_{j-1}^w\),要乘\(x_w\),而对于\(x_w\),要乘\(\theta_{j-1}^w\),并求和。
基于Hierarchical Softmax的CBOW
对于从输入层到隐藏层(投影层):对\(w\)周围的\(2c\)个词向量求和取平均即可:
\[
x_w = \frac{1}{2c}\sum\limits_{i=1}^{2c}x_i
\]
然后通过梯度上升法来更新\(\theta_{j-1}^w\)和\(x_w\),因为\(x_w\)是\(2c\)个向量求和得到的,所以梯度更新后,会用同一个梯度项(即下面提到的\(e\))直接更新原始的各个\(x_i(i=1,2,...,2c)\),即:
\[
\begin{align*}
\theta_{j-1}^w &= \theta_{j-1}^w + \eta (1-d_j^w-\sigma(x_w^T\theta_{j-1}^w))x_w \\
x_w &= x_w +\eta \sum\limits_{j=2}^{l_w}(1-d_j^w-\sigma(x_w^T\theta_{j-1}^w))\theta_{j-1}^w \;(i =1,2..,2c) \\
\end{align*}
\]
总结:
- 输入:词向量的维度大小为
\(M\),CBOW的上下文大小为\(2c\),步长\(\eta\) - 输出:哈夫曼树内部节点模型参数
\(\theta\),所有词向量\(w\)
- 基于语料训练样本建立哈夫曼树。
- 随机初始化所有的模型参数
\(\theta\),所有的词向量\(w\)。- 对于训练集中的每一个样本
\((context(w), w)\):
\(e=0\)计算\(x_w= \frac{1}{2c}\sum\limits_{i=1}^{2c}x_i\)- for
\(j=2,3,...,l_w\),计算\[ \begin{align*} f &= \sigma(x_w^T\theta_{j-1}^w) \\ g &= (1-d_j^w-f)\eta \\ e &= e + g\theta_{j-1}^w \\ \theta_{j-1}^w&= \theta_{j-1}^w + gx_w \\ \end{align*} \]- 对于
\(context(w)\)中的每一个词向量\(x_i\)(共有\(2c\)个)进行更新:\[ x_i = x_i + e \]- 如果梯度收敛,则结束梯度迭代,否则回到步骤3继续迭代。
基于Hierarchical Softmax的Skip-Gram
输入的只有一个词\(w\),输出的是\(2c\)个词向量\(context(w)\)
对于从输入层到隐藏层(投影层),这一步比CBOW简单,由于只有一个词,所以,即\(x_w\)就是词\(w\)对应的词向量。
然后通过梯度上升法来更新\(\theta_{j-1}^w\)和\(x_w\),这里的\(x_w\)周围有\(2c\)个词向量,有两种处理方式:
- 期望
\(P(x_i|x_w), i=1,2...2c\)最大。也就是从\(x_w\)出发,走到第\(i\)个词,需要走\(2c\)条路径 - 期望
\(P(x_w|x_i), i=1,2...2c\)最大。也就是对于每个\(i\),从\(x_i\)出发,走到同一个终点\(x_w\),同样是\(2c\)条路径。
word2vec中,使用了\(P(x_w|x_i)\)。这样一来,在一个迭代窗口内,不是只更新\(x_w\)一个词,而是\(x_i,i=1,2,...,2c\)共\(2c\)个词。这样整体的迭代会更加的均衡。因此,Skip-Gram模型并没有和CBOW模型一样对输入进行迭代更新,而是对\(2c\)个输出进行迭代更新。
总结:
- 输入:基于Skip-Gram的语料训练样本,词向量的维度大小
\(M\),Skip-Gram的上下文大小\(2c\),步长\(\eta\) - 输出:哈夫曼树的内部节点模型参数
\(\theta\),所有的词向量\(w\)
- 基于语料训练样本建立哈夫曼树。
- 随机初始化所有的模型参数
\(\theta\),所有的词向量\(w\)。- 对于训练集中的每一个样本
\((w, context(w))\):
- for
\(i=1,2,...,2c\)
\(e=0\)- for
\(j=2,3,...,l_w\),计算\[ \begin{align*} f &= \sigma(x_i^T\theta_{j-1}^w) \\ g &= (1-d_j^w-f)\eta \\ e &= e + g\theta_{j-1} \\ \theta_{j-1}^w&= \theta_{j-1}^w + gx_i \\ \end{align*} \]- 进行完
\(j\)的for循环后,更新一次\(x_i\)\[ x_i = x_i + e \]- 进行完
\(i\)的for循环后,如果梯度收敛,则结束梯度迭代,否则回到步骤3.1继续迭代。
hierarchical softmax源码解析
代码:https://github.com/tmikolov/word2vec/blob/master/word2vec.c
neu1e:相当于上面的\(e\)syn0:相当于上面的\(x_w\)syn1:相当于上面的\(\theta_{j-1}^i\)layer1_size:相当于上面的词向量的维度\(M\)window:相当于上面的\(c\)vocab[word].code[d]:当前单词word的,第d个编码,编码不含Root结点vocab[word].point[d]:当前单词word,第d个编码下,前置的结点
cbow + hs:
for (c = 0; c < layer1_size; c++) neu1[c] /= cw;
if (hs) for (d = 0; d < vocab[word].codelen; d++) {
f = 0;
l2 = vocab[word].point[d] * layer1_size;
// Propagate hidden -> output
for (c = 0; c < layer1_size; c++) f += neu1[c] * syn1[c + l2];
if (f <= -MAX_EXP) continue;
else if (f >= MAX_EXP) continue;
else f = expTable[(int)((f + MAX_EXP) * (EXP_TABLE_SIZE / MAX_EXP / 2))];
// 'g' is the gradient multiplied by the learning rate
g = (1 - vocab[word].code[d] - f) * alpha;
// Propagate errors output -> hidden
for (c = 0; c < layer1_size; c++) neu1e[c] += g * syn1[c + l2];
// Learn weights hidden -> output
for (c = 0; c < layer1_size; c++) syn1[c + l2] += g * neu1[c];
skipgram + hs:
if (hs) for (d = 0; d < vocab[word].codelen; d++) {
f = 0;
l2 = vocab[word].point[d] * layer1_size;
// Propagate hidden -> output
for (c = 0; c < layer1_size; c++) f += syn0[c + l1] * syn1[c + l2];
if (f <= -MAX_EXP) continue;
else if (f >= MAX_EXP) continue;
else f = expTable[(int)((f + MAX_EXP) * (EXP_TABLE_SIZE / MAX_EXP / 2))];
// 'g' is the gradient multiplied by the learning rate
g = (1 - vocab[word].code[d] - f) * alpha;
// Propagate errors output -> hidden
for (c = 0; c < layer1_size; c++) neu1e[c] += g * syn1[c + l2];
// Learn weights hidden -> output
for (c = 0; c < layer1_size; c++) syn1[c + l2] += g * syn0[c + l1];
}
4.2 负采样和nce
下文对nce有大概的讲解。先来重点看下负采样。
参考https://www.cnblogs.com/pinard/p/7249903.html
hs的一个缺点就是,如果我们的训练样本里的中心词\(w\)是一个很生僻的词,那么就得在哈夫曼树中辛苦的向下走很久。
对于中心词\(w\)和他的上下文\(context(w)\),这是一个正例。可以采集neg个\(w_i, i=1,2,..neg\),这样分别和\(context(w)\)可以构成neg个负例。然后利用这些正负例,进行二元logistic regression,得到负采样的每个\(w_i\)对应的模型参数\(\theta_i\),和每个词的词向量。
Negative Sampling梯度计算
定义正例为\(w_0\),neg个负例为\(w_i, i=1,2,..neg\)。
正例的概率和label是:
\[
P(context(w_0), w_i) = \sigma(x_{w_0}^T\theta^{w_i}) ,y_i=1, i=0
\]
负例的概率和label是:
\[
P(context(w_0), w_i) =1- \sigma(x_{w_0}^T\theta^{w_i}), y_i = 0, i=1,2,..neg
\]
期望能最大化:
\[
\prod_{i=0}^{neg}P(context(w_0), w_i) = \sigma(x_{w_0}^T\theta^{w_0})\prod_{i=1}^{neg}(1- \sigma(x_{w_0}^T\theta^{w_i}))
\]
所以似然函数是:
\[
\prod_{i=0}^{neg} \sigma(x_{w_0}^T\theta^{w_i})^{y_i}(1- \sigma(x_{w_0}^T\theta^{w_i}))^{1-y_i}
\]
对应的对数似然函数就是:
\[
L = \sum\limits_{i=0}^{neg}y_i log(\sigma(x_{w_0}^T\theta^{w_i})) + (1-y_i) log(1- \sigma(x_{w_0}^T\theta^{w_i}))
\]
与hs类似,需要对\(x_{w_i}\)和\(\theta^{w_i}, i=0,1,..neg\)这两大参数进行更新:
\(\theta^{w_i}\)的梯度如下:
\[
\begin{align*}
\frac{\partial L}{\partial \theta^{w_i} } &= y_i(1- \sigma(x_{w_0}^T\theta^{w_i}))x_{w_0}-(1-y_i)\sigma(x_{w_0}^T\theta^{w_i})x_{w_0} \\
& = (y_i -\sigma(x_{w_0}^T\theta^{w_i})) x_{w_0}
\end{align*}
\]
同样地,\(x_{w_0}\)的梯度如下:
\[
\frac{\partial L}{\partial x_{w_0} } = \sum\limits_{i=0}^{neg}(y_i -\sigma(x_{w_0}^T\theta^{w_i}))\theta^{w_i}
\]
Negative Sampling负采样方法
如果词汇表的大小为\(V\),那么我们将一段长度为1的线段分成\(V\)份,每份对应词汇表中的一个词。高频词对应的线段长,低频词对应的线段短(和轮盘赌有异曲同工之妙)。每个词\(w\)的线段长度由下式决定:
\[
len(w) = \frac{count(w)}{\sum\limits_{u \in vocab} count(u)}
\]
word2vec中,分子和分母都取了3/4次幂:
\[
len(w) = \frac{count(w)^{3/4}}{\sum\limits_{u \in vocab} count(u)^{3/4}}
\]
采样前,我们将这段长度为1的线段划分\(M\)等份,\(M >> V\)。这样可以保证每个词对应的线段都会划分成对应的小块。M份中的每一份都会落在某一个词对应的线段上。
采样的时候,我们只需要从\(M\)个位置中采样出neg个位置就行,此时采样到的每一个位置对应到的线段所属的词就是我们的负例词。
在word2vec中,\(M\)取值默认为\(10^8\)。
基于Negative Sampling的CBOW模型
- 输入:基于CBOW的语料训练样本,词向量的维度大小
\(M\),CBOW的上下文大小\(2c\),步长\(\eta\), 负采样的个数neg - 输出:词汇表每个词对应的模型参数
\(\theta\),所有的词向量\(x_w\)
- 随机初始化所有的模型参数
\(\theta\),所有的词向量\(w\)。- 对于训练集中的每一个样本
\((context(w_0), w_0)\),负采样出neg个负例中心词\(w_i, i=1,2,...neg\)- 进行梯度上升迭代过程,对于训练集中的每一个样本
\((context(w_0), w_0,w_1,...w_{neg})\)做如下处理:
\(e=0\)计算\(x_{w_0}= \frac{1}{2c}\sum\limits_{i=1}^{2c}x_i\)- for
\(i=0,1,...,neg\),计算\[ \begin{align*} f &= \sigma(x_{w_0}^T\theta^{w_i}) \\ g &= (y_i-f)\eta \\ e &= e + g\theta^{w_i} \\ \theta^{w_i}&= \theta^{w_i} + gx_{w_0} \\ \end{align*} \]- 对于
\(context(w)\)中的每一个词向量\(x_k\)(共有\(2c\)个)进行更新:\[ x_k = x_k + e \]- 如果梯度收敛,则结束梯度迭代,否则回到步骤3继续迭代。
基于Negative Sampling的Skip-Gram模型
- 输入:基于Skip-Gram的语料训练样本,词向量的维度大小
\(M\),Skip-Gram的上下文大小\(2c\),步长\(\eta\),负采样的个数neg - 输出:词汇表每个词对应的模型参数
\(\theta\),所有的词向量\(x_w\)
- 随机初始化所有的模型参数
\(\theta\),所有的词向量\(w\)。- 对于训练集中的每一个样本
\((context(w_0), w_0)\),负采样出neg个负例中心词\(w_i, i=1,2,...neg\)- 进行梯度上升迭代过程,对于训练集中的每一个样本
\((context(w_0), w_0,w_1,...w_{neg})\)做如下处理:
- for
\(i=1,2,...,2c\)
\(e=0\)- for
\(j=0,1,...,neg\),计算\[ \begin{align*} f &= \sigma(x_{w_{0i}}^T\theta^{w_j}) \\ g &= (y_j-f)\eta \\ e &= e + g\theta^{w_j} \\ \theta^{w_j} &= \theta^{w_j} + gx_{w_{0i}} \\ \end{align*} \]- 进行完
\(j\)的for循环后,更新一次\(x_{w_{0i}}\)\[ x_{w_{0i}} = x_{w_{0i}} + e \]- 进行完
\(i\)的for循环后,如果梯度收敛,则结束梯度迭代,否则回到步骤3.1继续迭代。
negative sampling源码解析
代码:https://github.com/tmikolov/word2vec/blob/master/word2vec.c
neu1e:相当于上面的\(e\)syn0:相当于上面的\(x_w\)syn1neg:相当于上面的\(\theta^{w_i}\)layer1_size:相当于上面的词向量的维度\(M\)window:相当于上面的\(c\)negative:相当于上面的negtable_size:相当于上面讲负采样时提到的划分数\(M\)vocab[word].code[d]:当前单词word的,第d个编码,编码不含Root结点vocab[word].point[d]:当前单词word,第d个编码下,前置的结点
cbow + negative sampling:
if (negative > 0) for (d = 0; d < negative + 1; d++) {
if (d == 0) {
target = word;
label = 1;
} else {
next_random = next_random * (unsigned long long)25214903917 + 11;
target = table[(next_random >> 16) % table_size];
if (target == 0) target = next_random % (vocab_size - 1) + 1;
if (target == word) continue;
label = 0;
}
l2 = target * layer1_size;
f = 0;
for (c = 0; c < layer1_size; c++) f += neu1[c] * syn1neg[c + l2];
if (f > MAX_EXP) g = (label - 1) * alpha;
else if (f < -MAX_EXP) g = (label - 0) * alpha;
else g = (label - expTable[(int)((f + MAX_EXP) * (EXP_TABLE_SIZE / MAX_EXP / 2))]) * alpha;
for (c = 0; c < layer1_size; c++) neu1e[c] += g * syn1neg[c + l2];
for (c = 0; c < layer1_size; c++) syn1neg[c + l2] += g * neu1[c];
}
skipgram + negative sampling:
if (negative > 0) for (d = 0; d < negative + 1; d++) {
if (d == 0) {
target = word;
label = 1;
} else {
next_random = next_random * (unsigned long long)25214903917 + 11;
target = table[(next_random >> 16) % table_size];
if (target == 0) target = next_random % (vocab_size - 1) + 1;
if (target == word) continue;
label = 0;
}
l2 = target * layer1_size;
f = 0;
for (c = 0; c < layer1_size; c++) f += syn0[c + l1] * syn1neg[c + l2];
if (f > MAX_EXP) g = (label - 1) * alpha;
else if (f < -MAX_EXP) g = (label - 0) * alpha;
else g = (label - expTable[(int)((f + MAX_EXP) * (EXP_TABLE_SIZE / MAX_EXP / 2))]) * alpha;
for (c = 0; c < layer1_size; c++) neu1e[c] += g * syn1neg[c + l2];
for (c = 0; c < layer1_size; c++) syn1neg[c + l2] += g * syn0[c + l1];
}
5. 面试常见问题
参考 https://blog.csdn.net/zhangxb35/article/details/74716245
x. tensorflow的简单实现
讲解:https://www.tensorflow.org/tutorials/word2vec
简介
使用maximum likelihood principle,最大化给定previous words \(h\),下一个词\(w_t\)的概率(使用softmax定义):
\[
\begin{align*}
P(w_t | h) &= \text{softmax} (\text{score} (w_t, h)) \\
&= \frac{\exp \{ \text{score} (w_t, h) \} }
{\sum_\text{Word w' in Vocab} \exp \{ \text{score} (w', h) \} }
\end{align*}
\]
需要最大化的对应的log-likelihood就是:
\[
\begin{align*}
J_\text{ML} &= \log P(w_t | h) \\
&= \text{score} (w_t, h) -
\log \left( \sum_\text{Word w' in Vocab} \exp \{ \text{score} (w', h) \} \right).
\end{align*}
\]
如果直接硬算,对于每个时间步,都需要遍历词典大小的空间,显然效率是不行的。在word2vec中,将这样一个多分类问题,变成了一个区分目标词\(w_t\)和k个noise words \(\tilde w\)的二分类问题。下图是cbow的示例,skipgram正好是倒过来。
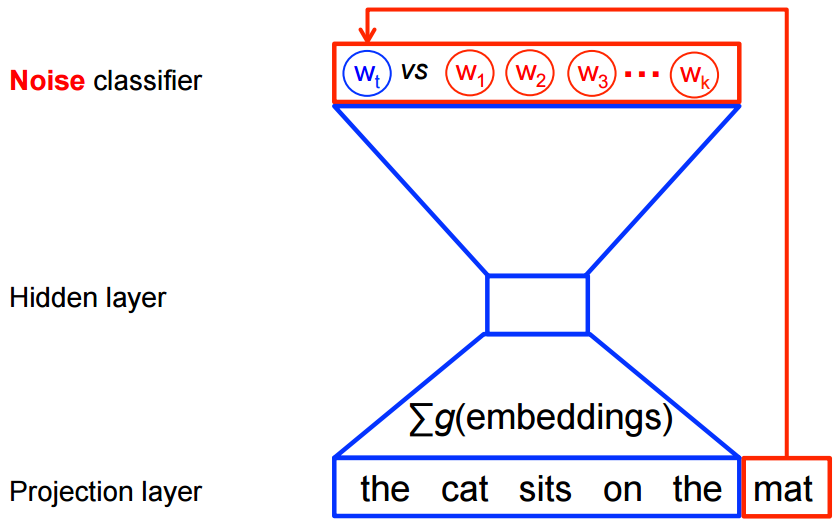
数学上,目标就是要最大化:
\[
J_\text{NEG} = \log Q_\theta(D=1 |w_t, h) +
k \mathop{\mathbb{E}}_{\tilde w \sim P_\text{noise}}
\left[ \log Q_\theta(D = 0 |\tilde w, h) \right]
\]
其中,\(Q_\theta(D=1 | w, h)\)是使用学到的embedding vector \(\theta\),在给定数据集\(D\)中的上下文\(h\),看到词\(w\)的概率。在实践中,我们通过从噪声分布中抽取\(k\)个对比词来逼近期望值(即计算蒙特卡洛平均值)。
直观地理解,这个目标就是希望预测为\(w_t\)的概率尽可能大,同时预测为非\(\tilde w\)的概率尽可能大,也就是,希望预测为真实词的概率尽量大,预测为noise word的概率尽量小。在极限情况下,这可以近似为softmax,但这计算量比softmax小很多。这就是所谓的negative sampling。
tensorflow有一个很类似的损失函数noise-contrastive estimation(NCE),即『噪声对比估算』,tf.nn.nce_loss()。
上面讲的是cbow,而skipgram其实也类似,假设拿一个词去预测周围的\(2C\)个词:
\[
\begin{align*}
J &= -\log p(w_{t-C},...,w_{t+C}|w_t) \\
&= -\log \prod ^{2C}_{c=1}\frac{\exp(u_{c,j^{*}_c})}{\sum ^V_{j=1} \exp(u_j)} \\
&= -\sum ^{2C}_{c=1}u_{j^{*}_c} + 2C \log\sum ^{V}_{j=1}\exp(u_j)
\end{align*}
\]
其中的\(\log\sum ^{V}_{j=1}\exp(u_j)\)部分,也可以用负采样和nce去搞。
针对句子
the quick brown fox jumped over the lazy dog
如果使用window_size=1(一个词左右各采一个词),那么对于CBOW,就有:
([the, brown], quick), ([quick, fox], brown), ([brown, jumped], fox), ...
而对于skipgram,则有:
(quick, the), (quick, brown), (brown, quick), (brown, fox), ...
在训练步\(t\)中,例如要用quick来预测the,我们从某个噪声分布(通常为一元分布\(P(w)\))中抽取num_noise个噪声对比样本。假设num_noise=1,并且将sheep选为噪声样本。那么在\(t\)时刻的目标是:
\[
J^{(t)}_\text{NEG} = \log Q_\theta(D=1 | \text{the, quick}) +
\log(Q_\theta(D=0 | \text{sheep, quick}))
\]
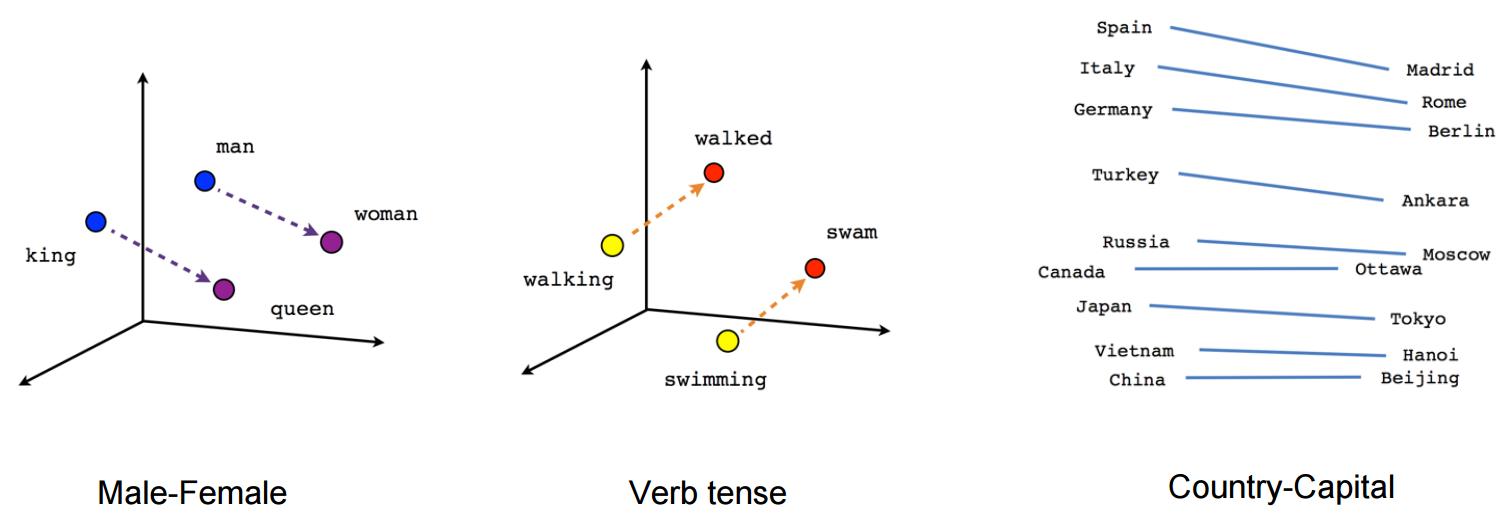
画图时,可以使用t-SNE的降维方法,将高维向量映射到2维空间。
代码解读
读数据
# Read the data into a list of strings.
def read_data(filename):
"""Extract the first file enclosed in a zip file as a list of words."""
with zipfile.ZipFile(filename) as f:
data = tf.compat.as_str(f.read(f.namelist()[0])).split()
return data
调用:
vocabulary = read_data(filename)
建立数据集
build一个dataset:
def build_dataset(words, n_words):
"""Process raw inputs into a dataset."""
count = [['UNK', -1]]
count.extend(collections.Counter(words).most_common(n_words - 1)) ## 取出词频top n_words-1的词,词频高的index小
dictionary = dict()
for word, _ in count:
dictionary[word] = len(dictionary)
data = list()
unk_count = 0
for word in words:
index = dictionary.get(word, 0)
if index == 0: # dictionary['UNK']
unk_count += 1
data.append(index)
count[0][1] = unk_count
reversed_dictionary = dict(zip(dictionary.values(), dictionary.keys()))
return data, count, dictionary, reversed_dictionary
调用:
data, count, dictionary, reverse_dictionary = build_dataset(
vocabulary, vocabulary_size)
生成skipgram的一个batch
生成一个batch的方法如下:
def generate_batch(batch_size, num_skips, skip_window):
global data_index
assert batch_size % num_skips == 0
assert num_skips <= 2 * skip_window
batch = np.ndarray(shape=(batch_size), dtype=np.int32)
labels = np.ndarray(shape=(batch_size, 1), dtype=np.int32)
span = 2 * skip_window + 1 # [ skip_window target skip_window ]
buffer = collections.deque(maxlen=span) # pylint: disable=redefined-builtin
if data_index + span > len(data):
data_index = 0
buffer.extend(data[data_index:data_index + span])
data_index += span
for i in range(batch_size // num_skips):
context_words = [w for w in range(span) if w != skip_window]
words_to_use = random.sample(context_words, num_skips)
for j, context_word in enumerate(words_to_use):
batch[i * num_skips + j] = buffer[skip_window]
labels[i * num_skips + j, 0] = buffer[context_word]
if data_index == len(data):
buffer.extend(data[0:span])
data_index = span
else:
buffer.append(data[data_index])
data_index += 1
# Backtrack a little bit to avoid skipping words in the end of a batch
data_index = (data_index + len(data) - span) % len(data)
return batch, labels
调用:
batch, labels = generate_batch(batch_size=8, num_skips=2, skip_window=1)
定义模型
placeholder等
先定义一下validation set
valid_size = 16 # Random set of words to evaluate similarity on.
valid_window = 100 # Only pick dev samples in the head of the distribution.
valid_examples = np.random.choice(valid_window, valid_size, replace=False)
然后定义一下input和label的placeholder:
graph = tf.Graph()
with graph.as_default():
# Input data.
with tf.name_scope('inputs'):
train_inputs = tf.placeholder(tf.int32, shape=[batch_size])
train_labels = tf.placeholder(tf.int32, shape=[batch_size, 1])
valid_dataset = tf.constant(valid_examples, dtype=tf.int32)
网络参数
定义:
- vocabulary_size x embedding_size的embedding
- vocabulary_size x embedding_size的nce_weights
- vocabulary_size的nce_biases
# Ops and variables pinned to the CPU because of missing GPU implementation
with tf.device('/cpu:0'):
# Look up embeddings for inputs.
with tf.name_scope('embeddings'):
embeddings = tf.Variable(
tf.random_uniform([vocabulary_size, embedding_size], -1.0, 1.0))
embed = tf.nn.embedding_lookup(embeddings, train_inputs)
# Construct the variables for the NCE loss
with tf.name_scope('weights'):
nce_weights = tf.Variable(
tf.truncated_normal(
[vocabulary_size, embedding_size],
stddev=1.0 / math.sqrt(embedding_size)))
with tf.name_scope('biases'):
nce_biases = tf.Variable(tf.zeros([vocabulary_size]))
loss
在NCE的实现中,使用的是log_uniform_candidate_sampler:
- 会在[0, range_max)中采样出一个整数k(k相当于词的id)
- P(k) = (log(k + 2) - log(k + 1)) / log(range_max + 1)
\[
\begin{aligned}
P(k)&=\frac{1}{log(range\_max+1)}log(\frac{k+2}{k+1}) \\
&= \frac{1}{log(range\_max+1)}log(1+\frac{1}{k+1}) \\
\end{aligned}
\]
k越大,被采样到的概率越小。而我们的词典中,可以发现词频高的index小,所以高词频的词会被优先采样为负样本。
下面定义loss
with tf.name_scope('loss'):
loss = tf.reduce_mean(
tf.nn.nce_loss(
weights=nce_weights,
biases=nce_biases,
labels=train_labels,
inputs=embed,
num_sampled=num_sampled,
num_classes=vocabulary_size))
# Construct the SGD optimizer using a learning rate of 1.0.
with tf.name_scope('optimizer'):
optimizer = tf.train.GradientDescentOptimizer(1.0).minimize(loss)
计算cos
只是为了看看迭代过程中,validtion set里每个词最近的topk词,看看效果。
# Compute the cosine similarity between minibatch examples and all embeddings.
norm = tf.sqrt(tf.reduce_sum(tf.square(embeddings), 1, keep_dims=True))
normalized_embeddings = embeddings / norm
## 使用valid_dataset做输入,normalized_embeddings做参数,进行lookup得到的emb
valid_embeddings = tf.nn.embedding_lookup(normalized_embeddings,
valid_dataset)
# (valid_size, emb_size) x (emb_size, vocab_size) = (valid_size, vocab_size)
# 因为valid_emb和norm_emb都是emb/norm(emb),所以两者的乘积就是cos
similarity = tf.matmul(
valid_embeddings, normalized_embeddings, transpose_b=True)
其他
# Merge all summaries.
merged = tf.summary.merge_all()
# Add variable initializer.
init = tf.global_variables_initializer()
# Create a saver.
saver = tf.train.Saver()
训练
with tf.Session(graph=graph) as session:
# Open a writer to write summaries.
writer = tf.summary.FileWriter(FLAGS.log_dir, session.graph)
# We must initialize all variables before we use them.
init.run()
print('Initialized')
average_loss = 0
for step in xrange(num_steps):
batch_inputs, batch_labels = generate_batch(batch_size, num_skips,
skip_window)
feed_dict = {train_inputs: batch_inputs, train_labels: batch_labels}
# Define metadata variable.
run_metadata = tf.RunMetadata()
# We perform one update step by evaluating the optimizer op (including it
# in the list of returned values for session.run()
# Also, evaluate the merged op to get all summaries from the returned "summary" variable.
# Feed metadata variable to session for visualizing the graph in TensorBoard.
_, summary, loss_val = session.run(
[optimizer, merged, loss],
feed_dict=feed_dict,
run_metadata=run_metadata)
average_loss += loss_val
# Add returned summaries to writer in each step.
writer.add_summary(summary, step)
# Add metadata to visualize the graph for the last run.
if step == (num_steps - 1):
writer.add_run_metadata(run_metadata, 'step%d' % step)
if step % 2000 == 0:
if step > 0:
average_loss /= 2000
# The average loss is an estimate of the loss over the last 2000 batches.
print('Average loss at step ', step, ': ', average_loss)
average_loss = 0
# Note that this is expensive (~20% slowdown if computed every 500 steps)
if step % 10000 == 0:
sim = similarity.eval()
for i in xrange(valid_size):
valid_word = reverse_dictionary[valid_examples[i]]
top_k = 8 # number of nearest neighbors
nearest = (-sim[i, :]).argsort()[1:top_k + 1]
log_str = 'Nearest to %s:' % valid_word
for k in xrange(top_k):
close_word = reverse_dictionary[nearest[k]]
log_str = '%s %s,' % (log_str, close_word)
print(log_str)
final_embeddings = normalized_embeddings.eval()
# Write corresponding labels for the embeddings.
with open(FLAGS.log_dir + '/metadata.tsv', 'w') as f:
for i in xrange(vocabulary_size):
f.write(reverse_dictionary[i] + '\n')
# Save the model for checkpoints.
saver.save(session, os.path.join(FLAGS.log_dir, 'model.ckpt'))
# Create a configuration for visualizing embeddings with the labels in TensorBoard.
config = projector.ProjectorConfig()
embedding_conf = config.embeddings.add()
embedding_conf.tensor_name = embeddings.name
embedding_conf.metadata_path = os.path.join(FLAGS.log_dir, 'metadata.tsv')
projector.visualize_embeddings(writer, config)
writer.close()
可视化
# Function to draw visualization of distance between embeddings.
def plot_with_labels(low_dim_embs, labels, filename):
assert low_dim_embs.shape[0] >= len(labels), 'More labels than embeddings'
plt.figure(figsize=(18, 18)) # in inches
for i, label in enumerate(labels):
x, y = low_dim_embs[i, :]
plt.scatter(x, y)
plt.annotate(
label,
xy=(x, y),
xytext=(5, 2),
textcoords='offset points',
ha='right',
va='bottom')
plt.savefig(filename)
try:
# pylint: disable=g-import-not-at-top
from sklearn.manifold import TSNE
import matplotlib.pyplot as plt
tsne = TSNE(
perplexity=30, n_components=2, init='pca', n_iter=5000, method='exact')
plot_only = 500
low_dim_embs = tsne.fit_transform(final_embeddings[:plot_only, :])
labels = [reverse_dictionary[i] for i in xrange(plot_only)]
plot_with_labels(low_dim_embs, labels, os.path.join(gettempdir(), 'tsne.png'))
except ImportError as ex:
print('Please install sklearn, matplotlib, and scipy to show embeddings.')
print(ex)
y1. tensorflow的高级实现1
如果您发现模型在输入数据方面存在严重瓶颈,您可能需要针对您的问题实现自定义数据读取器
https://github.com/tensorflow/models/blob/master/tutorials/embedding/word2vec.py
y2. tensorflow的高级实现2
如果您的模型不再受 I/O 限制,但您仍希望提高性能,则可以通过编写自己的 TensorFlow 操作(如添加新操作中所述)进一步采取措施:
https://github.com/tensorflow/models/blob/master/tutorials/embedding/word2vec_optimized.py
自己的总结
某个时候整理了个ppt:

原创文章,转载请注明出处!
本文链接:http://daiwk.github.io/posts/nlp-word2vec.html