tensorflow代码解析——概览

首页 > 常用平台 > 正文

tensorflow代码解析——概览

标签：tensorflow代码, 代码解析, 概览

2018-04-07

简介
- 总体结构
- 代码结构
tf核心概念

参考：

简介

总体结构

从底向上分为设备管理和通信层、数据操作层、图计算层、API接口层、应用层。

底层设备通信层负责网络通信和设备管理。
- 设备管理可以实现TF设备异构的特性，支持CPU、GPU、Mobile等不同设备。
- 网络通信依赖gRPC通信协议实现不同设备间的数据传输和更新。
数据操作层是Tensor的OpKernels实现。这些OpKernels以Tensor为处理对象，依赖网络通信和设备内存分配，实现了各种Tensor操作或计算。Opkernels不仅包含MatMul等计算操作，还包含Queue等非计算操作
图计算层（Graph），包含本地计算流图和分布式计算流图的实现。Graph模块包含Graph的创建、编译、优化和执行等部分，Graph中每个节点都是OpKernels类型表示。
API接口层。Tensor C API是对TF功能模块的接口封装，便于其他语言平台调用。
应用层。不同编程语言在应用层通过API接口层调用TF核心功能实现相关实验和应用。

代码结构

以2018.09.23的master为基准:

tensorflow/core

其中，tensorflow/core目录包含了TF核心模块代码：

public: API接口头文件目录，用于外部接口调用的API定义，主要是session.h。
client: API接口实现文件目录。（目前已经没有这个目录了…）
platform: OS系统相关接口文件，如file system, env等。
protobuf: 均为.proto文件，用于数据传输时的结构序列化。（都是proto3的语法）
common_runtime: 公共运行库，包含session, executor, threadpool, rendezvous, memory管理, 设备分配算法等。
distributed_runtime: 分布式执行模块，如rpc session, rpc master, rpc worker, graph manager。
framework: 包含基础功能模块，如log, memory, tensor
graph: 计算流图相关操作，如construct, partition, optimize, execute等
kernels: 核心Op，如matmul, conv2d, argmax, batch_norm等
lib: 公共基础库，如gif、gtl(google模板库)、hash、histogram、jpeg、png、wav等。
ops: 基本ops运算(xxx_ops.cc)，ops梯度运算（xxx_grad.cc），io相关的ops（io_ops.cc），控制流和数据流*操作（control_flow_ops.cc和data_flow_ops.cc）

tensorflow/stream_executor

tensorflow/stream_executor目录是并行计算框架，由google stream executor团队开发。

tensorflow/contrib

tensorflow/contrib目录是contributor开发目录。

tensroflow/python

tensroflow/python目录是python API客户端脚本

third_party

eigen3：eigen矩阵运算库，tf基础ops调用
gpus: 封装了cuda/cudnn编程库

tf核心概念

tf的核心是围绕Graph展开的，简而言之，就是Tensor沿着Graph传递闭包完成Flow的过程。

Tensor

Matrix表示二维线性映射，Tensor表示多维线性映射。TF中Tensor的维数描述为阶，数值是0阶，向量是1阶，矩阵是2阶，以此类推，可以表示n阶高维数据。

tensor contraction

matrix的product和tensor的contract运算如下：

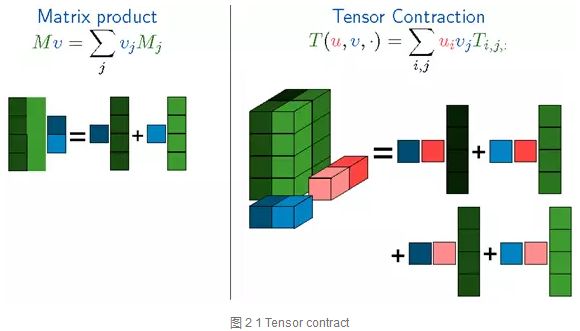
可见，一个4x2的A与一个2x1的B矩阵相乘，可以变成两个矩阵相加，每一个是一个1x1与一个4x1相乘，就是A矩阵的两列分别与B的两列分别相乘，再相加

contract是tensor的运算，python实现可以看：tensorflow/tensorflow/python/ops/math_ops.py，即tensordot（也称为张量收缩）对从a和b所指定的索引a_axes和b_axes的元素的乘积进行求和。a_axes和b_axes是两个数组，指定沿其收缩张量的那些轴对。对于所有range(0, len(a_axes))中的i，a的轴a_axes[i]必须与b的轴b_axes[i]具有相同的维度。列表a_axes和b_axes必须具有相同的长度，并由唯一的整数组成，用于为每个张量指定有效的坐标轴。

该操作对应于numpy.tensordot(a, b, axes)，numpy.tensordot文档。

示例1：当a和b是矩阵（2阶）时，axes = 1相当于矩阵乘法。
示例2：当a和b是矩阵（2阶）时，axes = [[1], [0]]相当于矩阵乘法。
示例3：假设\(a_ {ijk}\)和\(b_ {lmn}\)表示3阶的两个张量。那么，contract(a, b, [[0], [2]])是4阶张量\(c_ {jklm}\)，其条目对应于索引\((j,k,l,m)\)由下式给出：

\[ c_{jklm} = \sum_i a_{ijk} b_{lmi} \]

可见，因为传入的是[[0],[2]]，所以ijk的第0维，即i，和lmn的第2维，即n，都变成了i，然后求和~

一般来说，order(c) = order(a) + order(b) - 2*len(axes[0])。

Tensor实现

Tensor在高维空间数学运算比Matrix计算复杂，计算量也非常大，加速张量并行运算是TF优先考虑的问题，如add, contract, slice, reshape, reduce, shuffle等运算。

TF中Tensor支持的数据类型有很多，如tf.float16, tf.float32, tf.float64, tf.uint8, tf.int8, tf.int16, tf.int32, tf.int64, tf.string, tf.bool, tf.complex64等，所有Tensor运算都使用*泛化的数据类型`*(可以重载*和+运算咯)表示。

Tensor定义和运算主要是调用Eigen矩阵计算库完成的。

Tensor的定义在tensorflow/core/framework/tensor.h中。

Tensor的两个主要的成员变量

TensorShape shape_;
TensorBuffer* buf_;

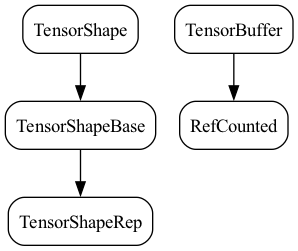
TensorShape在tensorflow/core/framework/tensor_shape.h中定义，基类是TensorShapeBase：

class TensorShape : public TensorShapeBase<TensorShape>

TensorShapeBase如下：

/// Represents the shape of a Tensor.
///
/// A tensor's shape is denoted by its number of dimensions and a size for each
/// dimension.  For example, a Tensor represented by a 3 x 4 matrix would have
/// a shape of 2-D, [3,4].
///
/// If you know the exact shape of your Tensor when you create the TensorShape
/// object, you can specify it then, or you can create a TensorShape with
/// zero dimensions and one element, and call AddDim() to add dimensions later.
class TensorShape : public TensorShapeBase<TensorShape> {
 public:
  using TensorShapeBase<TensorShape>::TensorShapeBase;

  /// Allow a TensorShape to be used as a PartialTensorShape without copying
  operator const PartialTensorShape&() const;  // NOLINT(runtime/explicit)

  /// Returns true if `*this` and `b` have the same sizes. Ignores
  /// dimension names.
  bool IsSameSize(const TensorShape& b) const;
  bool operator==(const TensorShape& b) const { return IsSameSize(b); }
  bool operator!=(const TensorShape& b) const { return !IsSameSize(b); }

  /// Fill `*dsizes` from `*this`.
  template <int NDIMS>
  Eigen::DSizes<Eigen::DenseIndex, NDIMS> AsEigenDSizes() const;

  /// Same as `AsEigenDSizes()` but allows for `NDIMS > dims()` -- in
  /// which case we pad the rest of the sizes with 1.
  template <int NDIMS>
  Eigen::DSizes<Eigen::DenseIndex, NDIMS> AsEigenDSizesWithPadding() const;

 private:
  // These CHECK fail to ease debugging.
  // REQUIRES: dims() == NDIMS
  void CheckDimsEqual(int NDIMS) const;
  // REQUIRES: dims() >= NDIMS
  void CheckDimsAtLeast(int NDIMS) const;
};

其中，TensorShapeBase是TensorShapeRep的子类

/// Base class for TensorShape and PartialTensorShape.
/// The class is templatized by either TensorShape or PartialTensorShape to
/// allow skipping known/unknown checks in the TensorShape case, but the
/// representation is shared exactly for fast conversion.
template <class Shape>
class TensorShapeBase : public TensorShapeRep

TensorBuffer是tensorflow/core/lib/core/refcount.h的RefCounted(引用计数器)的子类

class TensorBuffer : public core::RefCounted

Tensor的主要函数

返回Eigen::Tensor类型的主要函数：

  template <typename T>
  typename TTypes<T>::Vec vec() {
    return tensor<T, 1>();
  }
  // 其中，typedef Eigen::TensorMap<Eigen::Tensor<T, 1, Eigen::RowMajor, IndexType>, Eigen::Aligned> Vec;

  template <typename T>
  typename TTypes<T>::Matrix matrix() {
    return tensor<T, 2>();
  }
  // 其中，typedef Eigen::TensorMap<Eigen::Tensor<T, 2, Eigen::RowMajor, IndexType>, Eigen::Aligned> Matrix;

  template <typename T, size_t NDIMS>
  typename TTypes<T, NDIMS>::Tensor tensor();
  // 其中，typedef Eigen::TensorMap<Eigen::Tensor<T, NDIMS, Eigen::RowMajor, IndexType>, Eigen::Aligned> Tensor;

其中的TTypes定义在tensorflow/core/framework/tensor_types.h中，如下：

// Helper to define Tensor types given that the scalar is of type T.
template <typename T, int NDIMS = 1, typename IndexType = Eigen::DenseIndex>
struct TTypes {
  // Rank-<NDIMS> tensor of scalar type T.
  typedef Eigen::TensorMap<Eigen::Tensor<T, NDIMS, Eigen::RowMajor, IndexType>,
                           Eigen::Aligned>
      Tensor;
  typedef Eigen::TensorMap<
      Eigen::Tensor<const T, NDIMS, Eigen::RowMajor, IndexType>, Eigen::Aligned>
      ConstTensor;

  // Unaligned Rank-<NDIMS> tensor of scalar type T.
  typedef Eigen::TensorMap<Eigen::Tensor<T, NDIMS, Eigen::RowMajor, IndexType> >
      UnalignedTensor;
  typedef Eigen::TensorMap<
      Eigen::Tensor<const T, NDIMS, Eigen::RowMajor, IndexType> >
      UnalignedConstTensor;

  typedef Eigen::TensorMap<Eigen::Tensor<T, NDIMS, Eigen::RowMajor, int>,
                           Eigen::Aligned>
      Tensor32Bit;

  // Scalar tensor (implemented as a rank-0 tensor) of scalar type T.
  typedef Eigen::TensorMap<
      Eigen::TensorFixedSize<T, Eigen::Sizes<>, Eigen::RowMajor, IndexType>,
      Eigen::Aligned>
      Scalar;
  typedef Eigen::TensorMap<Eigen::TensorFixedSize<const T, Eigen::Sizes<>,
                                                  Eigen::RowMajor, IndexType>,
                           Eigen::Aligned>
      ConstScalar;

  // Unaligned Scalar tensor of scalar type T.
  typedef Eigen::TensorMap<
      Eigen::TensorFixedSize<T, Eigen::Sizes<>, Eigen::RowMajor, IndexType> >
      UnalignedScalar;
  typedef Eigen::TensorMap<Eigen::TensorFixedSize<const T, Eigen::Sizes<>,
                                                  Eigen::RowMajor, IndexType> >
      UnalignedConstScalar;

  // Rank-1 tensor (vector) of scalar type T.
  typedef Eigen::TensorMap<Eigen::Tensor<T, 1, Eigen::RowMajor, IndexType>,
                           Eigen::Aligned>
      Flat;
  typedef Eigen::TensorMap<
      Eigen::Tensor<const T, 1, Eigen::RowMajor, IndexType>, Eigen::Aligned>
      ConstFlat;
  typedef Eigen::TensorMap<Eigen::Tensor<T, 1, Eigen::RowMajor, IndexType>,
                           Eigen::Aligned>
      Vec;
  typedef Eigen::TensorMap<
      Eigen::Tensor<const T, 1, Eigen::RowMajor, IndexType>, Eigen::Aligned>
      ConstVec;

  // Unaligned Rank-1 tensor (vector) of scalar type T.
  typedef Eigen::TensorMap<Eigen::Tensor<T, 1, Eigen::RowMajor, IndexType> >
      UnalignedFlat;
  typedef Eigen::TensorMap<
      Eigen::Tensor<const T, 1, Eigen::RowMajor, IndexType> >
      UnalignedConstFlat;
  typedef Eigen::TensorMap<Eigen::Tensor<T, 1, Eigen::RowMajor, IndexType> >
      UnalignedVec;
  typedef Eigen::TensorMap<
      Eigen::Tensor<const T, 1, Eigen::RowMajor, IndexType> >
      UnalignedConstVec;

  // Rank-2 tensor (matrix) of scalar type T.
  typedef Eigen::TensorMap<Eigen::Tensor<T, 2, Eigen::RowMajor, IndexType>,
                           Eigen::Aligned>
      Matrix;
  typedef Eigen::TensorMap<
      Eigen::Tensor<const T, 2, Eigen::RowMajor, IndexType>, Eigen::Aligned>
      ConstMatrix;

  // Unaligned Rank-2 tensor (matrix) of scalar type T.
  typedef Eigen::TensorMap<Eigen::Tensor<T, 2, Eigen::RowMajor, IndexType> >
      UnalignedMatrix;
  typedef Eigen::TensorMap<
      Eigen::Tensor<const T, 2, Eigen::RowMajor, IndexType> >
      UnalignedConstMatrix;
};

用法如下：

    typedef float T;
    Tensor my_mat(...built with Shape{rows: 3, cols: 5}...);
    auto mat = my_mat.matrix<T>();    // 2D Eigen::Tensor, 3 x 5.
    auto mat = my_mat.tensor<T, 2>(); // 2D Eigen::Tensor, 3 x 5.
    auto vec = my_mat.vec<T>();       // CHECK fails as my_mat is 2D.
    auto vec = my_mat.tensor<T, 3>(); // CHECK fails as my_mat is 2D.
    auto mat = my_mat.matrix<int32>();// CHECK fails as type mismatch.

Eigen::Tensor

eigen源码：

https://bitbucket.org/eigen/eigen/src/8dd2d6552a87?at=default

git上的源码：

https://github.com/eigenteam/eigen-git-mirror

Eigen::Tensor不属于Eigen官方维护的程序，由贡献者提供文档和维护，所以Tensor定义在Eigen unsupported模块中(#include "third_party/eigen3/unsupported/Eigen/CXX11/Tensor")

参考http://eigen.tuxfamily.org/dox-devel/unsupported/classEigen_1_1Tensor.html

Tensor主要包含一个变量TensorStorage<Scalar, Dimensions, Options> m_storage，而TensorStorage里有两个变量m_data和m_dimensions，m_data保存了Tensor的数据块，T是泛化的数据类型，m_dimensions保存了Tensor的维度信息。

EIGEN_ALIGN_MAX T m_data[MinSize];
 FixedDimensions m_dimensions;

Eigen::Tensor的成员变量很简单，却支持非常多的基本运算，再借助Eigen的加速机制实现快速计算。Eigen::Tensor主要包含了

一元运算（Unary），如sqrt、square、exp、abs等。
二元运算（Binary），如add，sub，mul，div等
选择运算（Selection），即if / else条件运算
归纳运算（Reduce），如reduce_sum， reduce_mean等
几何运算（Geometry），如reshape，slice，shuffle，chip，reverse，pad，concatenate，extract_patches，extract_image_patches等
张量积（Contract）和卷积运算（Convolve）是重点运算，后续会详细讲解。

符号编程

编程模式通常分为命令式编程（imperative style programs）和符号式编程（symbolic style programs）。

命令式编程：容易理解和调试，命令语句基本没有优化，按原有逻辑执行。
符号式编程：涉及较多的嵌入和优化，不容易理解和调试，但运行速度有同比提升。

命令式编程明确输入变量，并根据程序逻辑逐步运算，这种模式非常在调试程序时进行单步跟踪，分析中间变量。

符号式编程将计算过程抽象为计算图，计算流图可以方便的描述计算过程，所有输入节点、运算节点、输出节点均符号化处理。

和目前的符号语言比起来，TF最大的特点是强化了数据流图，引入了mutation的概念。所谓mutation，就是可以在计算的过程中更改一个变量的值，而这个变量在计算的过程中会被带入到下一轮迭代里面去。mutation是机器学习优化算法几乎必须要引入的东西（虽然也可以通过immutable replacement来代替，但是会有效率的问题），这一点会导致最后的API设计和使用需要特别小心，把mutation引入到数据流图中会带来一些新的问题，比如，如何处理写与写之间的依赖。

梯度计算

梯度计算涉及每个计算节点，每个自定义的前向计算图都包含一个隐式的反向计算图。从数据流向上看，正向计算图是数据从输入节点到输出节点的流向过程，反向计算图是数据从输出节点到输入节点的流向过程。

可以参考tensorflow实战 chap1的自动求导部分

反向计算限制了符号编程中内存空间复用的优势，因为在正向计算中的计算数据在反向计算中也可能要用到。从这一点上讲，粗粒度的计算节点比细粒度的计算节点更有优势，而TF大部分为细粒度操作，虽然灵活性很强，但细粒度操作涉及到更多的优化方案，在工程实现上开销较大，不及粗粒度简单直接。在神经网络模型中，TF将逐步侧重粗粒度运算。

控制流

TF的计算图如同数据流一样，数据流向表示计算过程。数据流图可以很好的表达计算过程，为了扩展TF的表达能力，TF中引入控制流。编程语言中，if…else…是最常见的逻辑控制，在TF的数据流中也可以通过这种方式控制数据流向。接口函数如下，pred为判别表达式，fn1和fn2为运算表达式。当pred为true是，执行fn1操作；当pred为false时，执行fn2操作。

tf.cond(pred, fn1, fn2, name=None)

TF还可以协调多个数据流，在存在依赖节点的场景下非常有用，例如节点B要读取模型参数\(\theta\)更新后的值，而节点A负责更新参数\(\theta\)，则节点B必须等节点A完成后才能执行，否则读取的参数\(\theta\)为更新前的数值，这时需要一个运算控制器。接口函数如下，tf.control_dependencies函数可以控制多个数据流执行完成后才能执行接下来的操作，通常与tf.group函数结合使用。

tf.control_dependencies(control_inputs)

TF支持的控制算子有Switch、Merge、Enter、Leave和NextIteration等。

TF不仅支持逻辑控制，还支持循环控制。TF使用和MIT Token-Tagged machine（即Executing a program on the MIT tagged-token dataflow architecture.）相似的表示系统，将循环的每次迭代标记为一个tag，迭代的执行状态标记为一个frame，但迭代所需的数据准备好的时候，就可以开始计算，从而多个迭代可以同时执行。

原创文章，转载请注明出处！
本文链接：http://daiwk.github.io/posts/platform-tensorflow-code-analysis-overview.html

上篇：自然语言处理中的自注意力机制（Self-Attention Mechanism）

下篇： tensorflow代码——数据持久化

comment here..