深入浅出强化学习-chap2 马尔科夫决策过程
标签:深入浅出强化学习, 马尔科夫决策过程, MDP, 值函数, 状态-行为值函数, 贝尔曼方程目录
参考《深入浅出强化学习》
1. 马尔科夫决策过程理论
1.1 马尔科夫性
系统的下一个状态\(s_{t+1}\)仅与当前状态\(s_t\)有关,与之前的状态无关。
定义:状态\(s_t\)是马尔科夫的,当且仅当\(P[s_{t+1}|s_t]=P[s_{t+1}|s_1,...,s_t]\)。
随机过程就是随机变量序列。如果随机变量序列的每个状态都是马尔科夫的,那么此随机过程就是马尔科夫随机过程。
1.2 马尔科夫过程
马尔科夫过程是一个二元组\((S,P)\),且满足:\(S\)是有限状态集合,\(P\)是状态转移概率。状态转移概率矩阵如下:
\[
P=\begin{bmatrix}
P_{11} & ... & P_{1n} \\
\vdots & \vdots & \vdots \\
P_{n1} & ... & P_{nn}
\end{bmatrix}
\]
由若干个状态组成的序列称为马尔科夫链。当给定状态转移概率时,从某个状态出发存在多条马尔科夫链。
1.3 马尔科夫决策过程
马尔科夫决策过程由元组\((S,A,P,R,\gamma)\)描述,其中:
\(S\)为有限的状态集\(A\)为有限的动作集\(P\)为状态转移概率\(R\)为回报函数\(\gamma\)为折扣因子,用于计算累积回报
区别于马尔科夫过程,马尔科夫决策过程的态转移概率是包含动作的,即\(P^a_{ss'}=P[S_{t+1}=s'|S_t=s,A_t=a]\)。
强化学习的目标是给定一个马尔科夫决策过程,寻找最优策略。策略指的是,状态到动作的映射,用符号\(\pi\)表示,给定状态\(s\)时,动作集上的一个分布,即:
\[
\pi (a|s)=p[A_i=a|S_t=s]
\]
含义是,策略\(\pi\)在每个状态\(s\)指定一个动作概率。如果给出的策略\(\pi\)是确定性的,那么策略\(\pi\)在每个状态\(s\)指定一个确定的动作。注,\(\sum _{a\in A}\pi(s,a)=1\)
概率在强化学习中的作用:
- 强化学习的策略往往是随机策略。可以将探索耦合到采样的过程中。探索,指机器人尝试其他动作以便找到更好的策略。
- 实际应用中,存在各种噪声,这些噪声大都服从正态分布,可以用概率的知识去掉噪声。
给定一个策略\(\pi\)时,可以计算累积回报:
\[
G_t=R_{t+1}+\gamma R_{t+2}+...=\sum _{k=0}^{\infty }\gamma ^kR_{i+k+1}
\]
当给定策略\(\pi\)时,假设从状态\(s_t\)出发,可能有很多个状态序列,所以对应的\(G_t\)也有多个可能值。为了评价状态\(s_t\)的价值,需要一个确定的量来描述。而累积回报\(G_t\)是一个随机变量,不是确定值,但其期望是一个确定值,因此可以做为状态值函数的定义。
1.4 状态值函数与状态-行为值函数
当智能体采用策略\(\pi\)时,累积回报服从一个分布,累积回报在状态\(s\)处的期望值定义状态值函数:
\[
\upsilon _{\pi}(s)=E_{\pi}[\sum _{k=0}^{\infty }\gamma ^kR_{t+k+1}|S_t=s]
\]
注:状态值函数是与策略\(\pi\)相对应的,因为策略\(\pi\)决定了累积回报\(G\)的状态分布。
状态-行为值函数为:
\[
q_{\pi}(s,a)=E_{\pi}[\sum _{k=0}^{\infty}\gamma ^kR_{t+k+1}|S_t=s,A_t=a]
\]
1.5 状态值函数与状态-行为值函数的贝尔曼方程
贝尔曼方程(Bellman Equation)也被称作动态规划方程(Dynamic Programming Equation)。
状态值函数的贝尔曼方程:
\[
\begin{split}
\\\upsilon(S_t)&=\upsilon(s)=E[G_t|S_t=s]
\\&=E[R_{t+1}+\gamma R_{t+2}+...|S_t=s]
\\&=E[R_{t+1}+\gamma (R_{t+2}+\gamma R_{t+3}+...)|S_t=s]
\\&=E[R_{t+1}+\gamma G_{t+1}|S_t=s]
\\&=E[R_{t+1}+\gamma \upsilon(S_{t+1})|S_t=s]
\end{split}
\]
最后一个等号的证明(书P23,有小改……)
\[
\begin{split}
\\\upsilon(S_t)&=E_{S_t,S_{t+1},...}(R_{t+1}+\gamma G_{t+1}|S_t=s)
\\&=E_{S_t}(R_{t+1})+\gamma E_{S_{t+1},...}(G_{t+1})
\\&=E_{S_t}(R_{t+1}+\gamma \upsilon(S_{t+1}))
\\&=E(R_{t+1}+\gamma\upsilon(S_{t+1}))
\end{split}
\]
同理,状态-行为值函数的贝尔曼方程:
\[
q_{\pi}(s,a)=E_{\pi}[R_{t+1}+\gamma q(S_{t+1},A_{t+1})|S_t=s,A_t=a]
\]
状态值函数与状态-行为值函数的关系:
\[
\upsilon_{\pi}(s)=\sum_{a\in A}\pi(a|s)q_{\pi}(s,a)
\]
而(其中,\(P^a_{ss'}\)表示从状态\(s\)开始,采取行动\(a\),移动到状态\(s'\)的概率)
\[
q_{\pi}(s,a)=R^a_{s}+\gamma \sum _{s'}P^a_{ss'}\upsilon _{\pi}(s')
\]
因此,
\[
\upsilon_{\pi}(s)=\sum_{a\in A}\pi(a|s)(R^a_{s}+\gamma \sum_{s'\in S}P^a_{ss'}\upsilon_{\pi}(s'))
\]
而
\[
\upsilon_{\pi}(s')=\sum _{a'\in A}\pi(a'|s')q_{\pi}(s',a')
\]
所以,状态-行为值函数是:
\[
q_{\pi}(s,a)=R^a_{s}+\gamma \sum_{s'\in S}P^a_{ss'}\sum _{a'\in A}\pi(a'|s')q_{\pi}(s',a')
\]
示例:
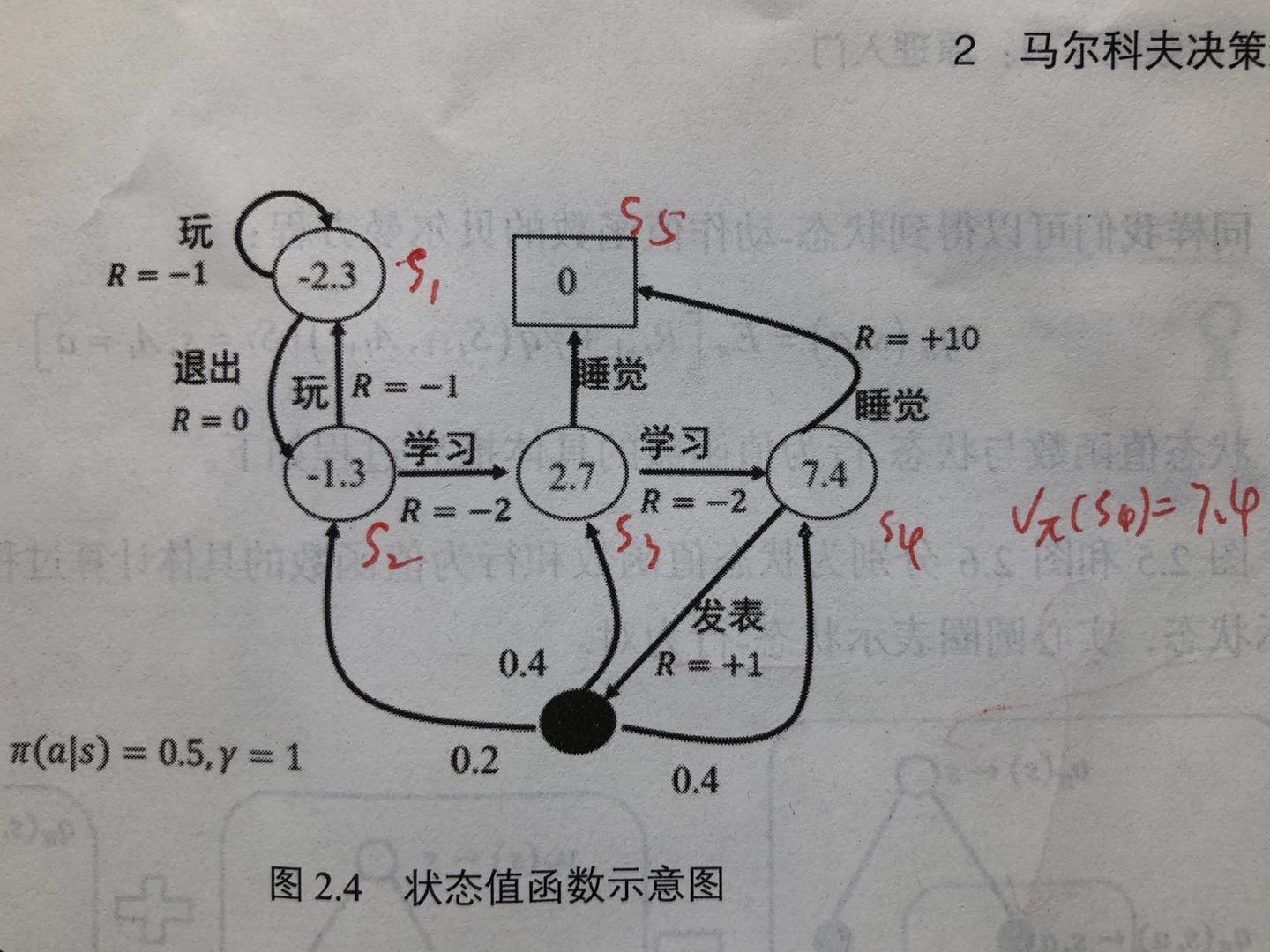
图中,空心圆圈中的数值为该状态下的值函数,实心圆圈表示状态-行为对。除了实心圆圈部分,其他状态转移\(\pi(a|s)=0.5,\gamma =1\)。\(s_4\)通过睡觉,可以到达\(s_5\),而通过发表,可以到达\(s_3\)、\(s_2\)和\(s_4\)
\[
\begin{split}
\\\upsilon (s_4)&=\pi(睡觉|s_4)R^{睡觉}_{s_4s_5}+\pi(发表|s_4)(R^{发表}_{s_4s_3}+\gamma (P^{发表}_{s_4s_2}\upsilon (s_2)+P^{发表}_{s_4s_3}\upsilon (s_3)+P^{发表}_{s_4s_4}\upsilon (s_4)))
\\&=0.5*10+0.5*(1+1*(0.2*(-1.3)+0.4*2.7+0.4*7.4))
\\&=7.39
\end{split}
\]
1.6 最优状态值函数与最优状态-行为值函数及其贝尔曼最优方程
每个策略对应一个状态值函数,最优策略对应着最优状态值函数。
定义:最优状态值函数\(\upsilon ^*(s)\)为在所有策略中值最大的值函数,即\(\upsilon ^*(s)=\underset{\pi}{max}\upsilon_{\pi}(s)\)。
最优状态-行为值函数\(q^*(s,a)\)为在所有策略中最大的状态-行为值函数,即\(q^*(s,a)=\underset{\pi}{max}q_{\pi}(s,a)\)。
从而,最优状态值函数的贝尔曼最优方程(与前面的\(\upsilon _{\pi}(s)\)的区别是,少乘了一个\(\pi(a|s)\)):
\[
\upsilon ^*(s)=\underset{a}{max}R^a_{s}+\gamma \sum _{s'\in S}P^a_{ss'}\upsilon ^*(s')
\]
最优状态-行为值函数的贝尔曼最优方程:
\[
q^*(s,a)=R^a_{s}+\gamma \sum _{s'\in S}P^a_{ss'}\underset{a'}{max}q^*(s',a')
\]
若已各大最优状态-值函数,最优策略可以通过直接最大化\(q^*(s,a)\)来决定:
\[
\pi_*(a|s)=\left\{\begin{matrix}
1 &if\ a=\underset{a\in A}{argmax}q_*(s,a) \\
0 & otherwise
\end{matrix}\right.
\]
1.7 强化学习形式化描述
定义一个离散时间有限范围的折扣马尔科夫决策过程\(M=(S,A,P,r,\rho_0,\gamma,T)\),
\(S\)为状态集\(A\)为动作集\(P:S\times A\times S\rightarrow R\)为转移概率\(r:S\times A\rightarrow [-R_{max},R_{max}]\)为立即回报函数\(\rho_0:S\rightarrow R\)是初始状态分布\(\gamma \in [0,1]\)是折扣因子\(T\)为水平范围(即步数)
\(\tau \)为一个轨迹序列,\(\tau =(s_0,a_0,s_1,a_1,...)\)
\(R=\sum _{t=0}^T\gamma ^tr_t\)为累积回报。
强化学习的目标是找到最优策略\(\pi\),使得该策略下的累积回报期望最大,即
\[
\underset{\pi}{max}\int R(\tau )p_{\pi}(\tau )d\tau
\]
2. MDP中的概率学基础
2.1 期望与方差
期望
函数f(x)关于某分布P(x)的期望指,当x由分布P(x)产生,f作用于x时,f(x)的平均值。
- 离散型随机变量的期望:
\[
E_{x\sim P}[f(x)]=\sum _xP(x)f(x)
\]
- 连续型随机变量的期望通过积分求得:
\[
E_{x\sim P}[f(x)]=\int p(x)f(x)dx
\]
期望的运算是线性的:
\[
E_x(\alpha f(x)+\beta g(x))=\alpha E_x[f(x)]+\beta E_x[g(x)]
\]
方差
方差衡量利用当前概率分布采样时,采样值差异的大小:
\[
Var(f(x))=E[(f(x)-E[f(x)])^2]
\]
方差越小,不确定性越小。
2.2 随机策略
2.2.1 贪婪策略
\[
\pi_*(a|s)=\left\{\begin{matrix}
1 &if\ a=\underset{a\in A}{argmax}q_*(s,a) \\
0 & otherwise
\end{matrix}\right.
\]
贪婪策略是一个确定性策略,只有动作值函数\(q^*(s,a)\)最大的动作时取概率1
2.2.2 \(\varepsilon -greedy\)策略
\[
\pi (a|s)=\left\{\begin{matrix}
1-\varepsilon + \frac{\varepsilon}{|A(s)|} &if\ a=\underset{a\in A}{argmax}q_*(s,a) \\
\frac{\varepsilon}{|A(s)|} & otherwise
\end{matrix}\right.
\]
\(\varepsilon -greedy\)策略是强化学习最基本最常用的随机策略。该策略平衡了e&e,也就是利用(exploitation)和探索(exploration),其中选取动作值函数最大的部分为利用,其他非最优动作仍然有概率的部分为探索部分。
也就是说,所有的\(\pi(a|s)\)都初始化为\(\frac{\varepsilon}{|A(s)|}\),而如果正好这个a能取到\(max_aQ(s,a)\),那么给他加上\((1-\varepsilon)\)
2.2.3 高斯策略
一般的高斯策略都可以写成
\[
\pi_{\theta}=\mu_{\theta}+\varepsilon,\varepsilon \sim N(0,\sigma ^2)
\]
其中\(\mu_{\theta}\)为确定性部分,\(\varepsilon\)为零均值的高斯随机噪声。这种策略也平衡了利用与探索,利用由确定性部分完成,探索由\(\varepsilon\)完成。
2.2.4 玻尔兹曼分布
对于动作空间是离散的,或者动作空间并不大的情况,可以采用玻尔兹曼分布(吉布斯分布)作为随机策略,即:
\[
\pi(a|s,\theta)=\frac{exp(Q(s,a,\theta))}{\sum_bexp(h(s,b,\theta))}
\]
其中,\(Q(s,a,\theta)\)是动作值函数。动作值函数大的动作被选中的概率大,小的动作被选中的概率小。
类似softmax,可以参考多类分类下为什么用softmax而不是用其他归一化方法?。
3. 基于gym的MDP实例
详见书p29
https://github.com/daiwk/reinforcement-learning-code/blob/master/grid_mdp.py
原创文章,转载请注明出处!
本文链接:http://daiwk.github.io/posts/rl-stepbystep-chap2.html