目录

• 1. 基于模型的动态方法理论
  • 1.1 动态规划
  • 1.2 策略迭代算法
    • 1.2.1 策略评估算法
    • 1.2.2 贪婪策略
    • 1.2.3 策略迭代算法
  • 1.3 值函数迭代算法
  • 1.4 解决最优控制问题的三种算法
    • 1.4.1 变分法原理
    • 1.4.2 庞特里亚金最大值原理
    • 1.4.3 动态规划方法
• 2. 动态规划中的数学基础
  • 2.1 线性方程组的迭代解法
  • 2.2 压缩映射证明策略评估的收敛性
• 3. 基于gym的编程实例
• 4. 最优控制与强化学习比较

参考《深入浅出强化学习》

1. 基于模型的动态方法理论

一个完整的已知模型的马尔科夫决策过程可以用元组\(S,A,P,r,\gamma\)表示。\(S\)为状态集，\(A\)为动作集，\(P\)为转移概率【对应环境和智能体的模型】，\(r\)为回报函数，\(\gamma\)为折扣因子，用于计算累积回报\(R=\sum_{t=0}^T\gamma ^tr_t\)。若\(T\)为有限值，强化学习过程称为有限范围强化学习。若\(T=\infty\)，称为无限范围强化学习。下面以有限范围强化学习为例。

强化学习的目标是找到最优策略\(\pi\)，使得累积回报的期望最大。策略是状态到动作的映射\(\pi:s\rightarrow a\)，\(\tau \)表示从状态\(s_t\)到最终状态\(s_T\)的一个序列\(\tau:s_t,s_{t+1},...,s_T\)，目标函数是累积回报函数的期望\(\int R(\tau)p_{\pi}(\tau)d\tau\)。

所以强化学习的目标是：\(\underset{\pi}{max}\int R(\tau)p_{\pi}(\tau)d\tau\)，最终目标是找到最优策略\(\pi ^*:s\rightarrow u^*\)。这里的\(u\)指的是决策序列\(u_0^*\rightarrow u_1^*\rightarrow ...u_T^*\)，所以，广义上来讲，强化学习就是找到一个决策序列，使得目标函数最优。

强化学习的分类如下图所示：

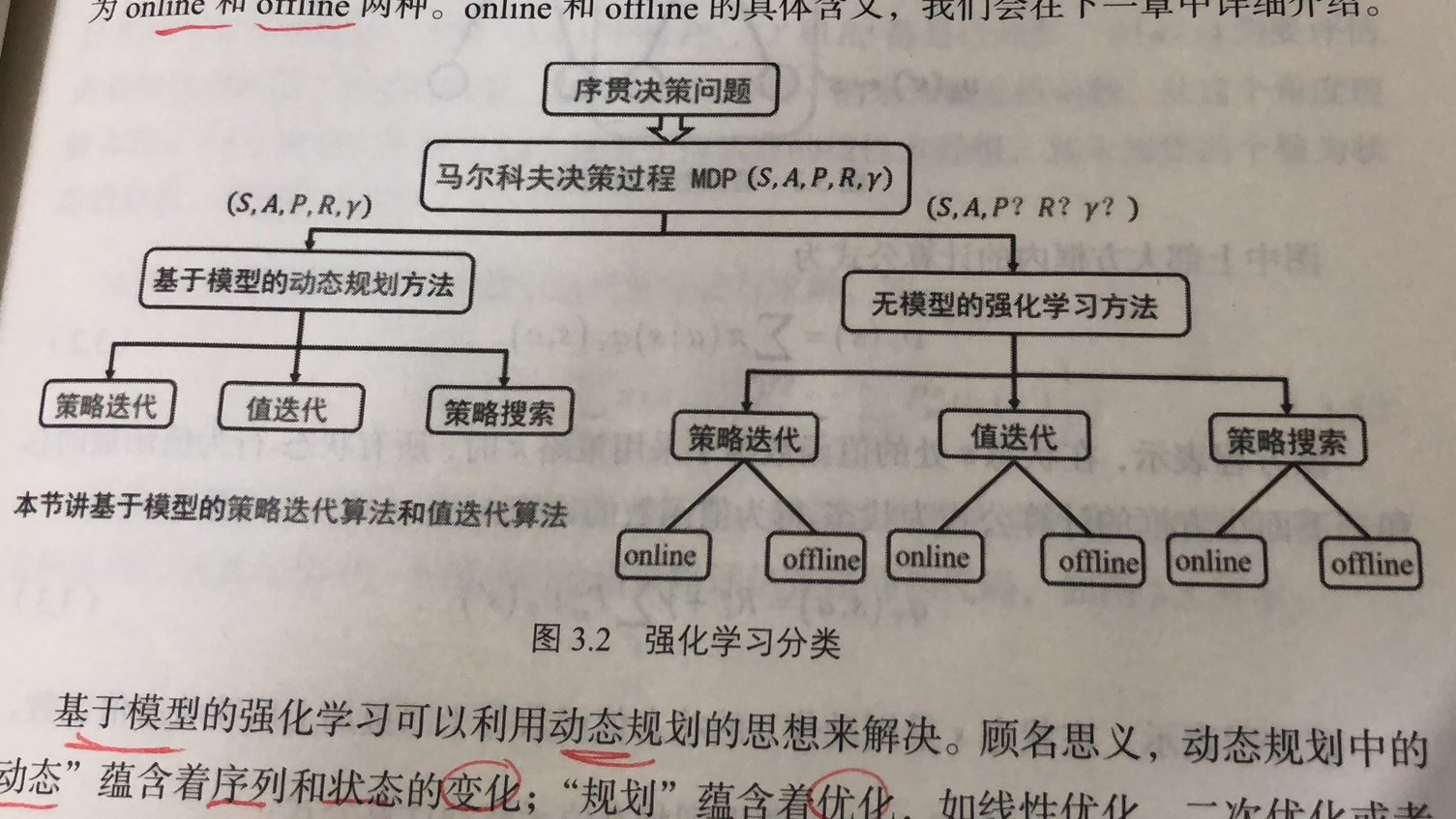
根据转移概率\(P\)是否已知，可以分为基于模型的动态规划方法，和基于无模型的强化学习方法。

这两种方法都包括策略迭代算法、值迭代算法和策略搜索算法。而基于无模型的强化学习方法中，每类方法又分为online和offline。

1.1 动态规划

基于模型的强化学习可以用动态规划的思想来解决。“动态”，指序列和状态的变化;“规划”，指优化，如线性优化、二次优化或非线性优化。

利用动态规划可解决的问题需要满足两个条件：

• 整个优化问题可以分解为多个子优化问题。
• 子优化问题的解可以被存储和重复利用。

第二章说到，强化学习可以利用马尔科夫决策过程来描述，利用贝尔曼最优性原理得到贝尔曼最优化方程：

\[ \\\upsilon ^*(s)=\underset{a}{max}R^a_{s}+\gamma \sum _{s'\in S}P^a_{ss'}\upsilon ^*(s') \\q^*(s,a)=R^a_{s}+\gamma \sum _{s'\in S}P^a_{ss'}\underset{a}{max}q^*(s',a') \]

可见马尔科夫决策问题符合使用动态规划的两个条件，所以可以用动态规划来解决。

动态规划的核心是找到最优值函数。

由上一章可以得到如下状态值函数的计算方法：

\[ \upsilon_{\pi}(s)=\sum_{a\in A}\pi(a|s)(R^a_{s}+\gamma \sum_{s'\in S}P^a_{ss'}\upsilon_{\pi}(s')) \]

从上式中可见，状态s处的值函数\(\upsilon_{\pi}(s)\)可以用后继状态的值函数\(\upsilon_{\pi}(s')\)来表示，而后继状态的值函数是未知的，所以这就是bootstrap算法。

上式中，对于模型已知的强化学习算法，\(P^a_{ss'}\)、\(\gamma\)和\(R^a_{s}\)都是已知的，\(\pi(a|s)\)是要评估的策略，是指定的，也是已知的。所以未知数就是值函数，未知数的个数为状态的总数，用\(|S|\)表示。

下面介绍如何求解上述公式(其实就是关于值函数的线性方程组)

1.2 策略迭代算法

1.2.1 策略评估算法

使用高斯-赛德尔迭代算法：

\[ \upsilon_{k+1}(s)=\sum_{a\in A}\pi(a|s)(R^a_{s}+\gamma \sum_{s'\in S}P^a_{ss'}\upsilon _{k}(s')) \]

算法步骤如下：

1. 输入：需要评估的策略\(\pi\)状态转移概率\(P^a_{ss'}\)回报函数\(R^a_s\)，折扣因子\(\gamma\)
2. 初始化值函数：\(\upsilon(s)=0\)
3. repeat k=0,1,…
4. for s in S:
5. \(\upsilon_{k+1}(s)=\sum _{a\in A}\pi(a|s)(R^a_{s}+\gamma \sum_{s'\in S}P^a_{ss'}\upsilon_k(s'))\)
6. until \(\upsilon_{k+1}=\upsilon_k\)
7. 输出：\(\upsilon(s)\)

注意：每次迭代都需要对状态集进行一次遍历，以评估每个状态的值函数。

1.2.2 贪婪策略

1.2.3 策略迭代算法

1.3 值函数迭代算法

1. 输入：状态转移概率\(P^a_{ss'}\)，回报函数\(R^a_{s}\)，折扣因子\(\gamma\)，初始化值函数\(\upsilon(s)=0\)，初始化策略\(\pi_0\)
2. Repeat \(l=0,1,...\)
3. for every \(s\) do
4. \(\upsilon _{l+1}(s)=\underset{a}{max}R^a_{s}+\gamma \sum _{s'\in S}P^a_{ss'}\upsilon _l(s')\)
5. Until \(\upsilon _{l+1}=\upsilon _l\)
6. 输出：\(\pi(s)=argmax_aR^a_{s}+\gamma \sum _{s'\in S}P^a_{ss'}\upsilon _l(s')\)

1.4 解决最优控制问题的三种算法

1.4.1 变分法原理

1.4.2 庞特里亚金最大值原理

1.4.3 动态规划方法

2. 动态规划中的数学基础

2.1 线性方程组的迭代解法

2.2 压缩映射证明策略评估的收敛性

3. 基于gym的编程实例

4. 最优控制与强化学习比较

上篇： TVM