目录

• l0范数
• l1范数
  • 概述
  • 稀疏的两个好处
  • 公式
• l2范数
  • 概述
  • l2的好处
• 常用图解释
• 不可导点的处理

参考http://blog.csdn.net/zouxy09/article/details/24971995

参考http://www.mamicode.com/info-detail-517504.html

l0范数

L0范数是指向量中非0的元素的个数，如果我们用L0范数来规则化一个参数矩阵W的话，就是希望W的大部分元素都是0，也就是，让参数W是稀疏的。

为什么不用L0，而要用L1呢？个人理解一是因为L0范数很难优化求解（NP难问题），二是L1范数是L0范数的最优凸近似，而且它比L0范数要容易优化求解。

l1范数

概述

l1(也叫Lasso regularization)可以使模型变得更sparse，因为它是L0范数的最优凸近似，任何的规则化算子，如果他在\(W_i=0\)的地方不可微，并且可以分解为一个“求和”的形式，那么这个规则化算子就可以实现稀疏。这说是这么说，W的L1范数是绝对值，\(|w|\)在w=0处是不可微

稀疏的两个好处

• 特征选择(Feature Selection)

一般来说，xi的大部分元素（也就是特征）都是和最终的输出yi没有关系或者不提供任何信息的，在最小化目标函数的时候考虑xi这些额外的特征，虽然可以获得更小的训练误差，但在预测新的样本时，这些没用的信息反而会被考虑，从而干扰了对正确yi的预测。稀疏规则化算子的引入就是为了完成特征自动选择的光荣使命，它会学习地去掉这些没有信息的特征，也就是把这些特征对应的权重置为0。

• 可解释性(Interpretability)

例如患某种病的概率是y，然后我们收集到的数据x是1000维的，也就是我们需要寻找这1000种因素到底是怎么影响患上这种病的概率的。假设我们这个是个回归模型：\(y=w1*x1+w2*x2+…+w1000*x1000+b\)（当然了，为了让y限定在[0,1]的范围，一般还得加个Logistic函数）。通过学习，如果最后学习到的\(w^*\)就只有很少的非零元素，例如只有5个非零的wi，那么我们就有理由相信，这些对应的特征在患病分析上面提供的信息是巨大的，决策性的。也就是说，患不患这种病只和这5个因素有关，那医生就好分析多了。但如果1000个wi都非0，医生面对这1000种因素，累觉不爱。

公式

假设有n个样本，在原始的cost function加上一项，即所有权重的绝对值的和乘以\(\frac{\lambda}{n}\)：

\[ C=C_0+\frac{\lambda }{n}\sum _w|w| \]

梯度如下，其中\(sgn(w)\)表示w的符号，即，w>0时，\(sgn(w)\)=1，w<0时，\(sgn(w)\)=-1：

\[ \frac{\partial C}{\partial w}=\frac{\partial C_0}{\partial w}+\frac{\lambda}{n}sgn(w) \]

权重更新如下：

\[ w=w-\frac{\eta \lambda}{n}sgn(w)-\eta \frac{\partial C_0}{\partial w} \]

比原始的更新规则多出了\(\frac{\eta \lambda}{n}sgn(w)\)这一项。当w为正时，更新后的w变小。当w为负时，更新后的w变大。因此它的效果就是让w往0靠，使网络中的权重尽可能为0，也就相当于减小了网络复杂度，防止过拟合。

当w等于0时，\(|w|\)是不可导的，所以我们只能按照原始的未经正则化的方法去更新w，这就相当于去掉\(\frac{\eta \lambda}{n}sgn(w)\)这一项，所以我们可以规定sgn(0)=0，这样就把w=0的情况也统一进来了。

l2范数

概述

用上l2的回归也叫“岭回归”（Ridge Regression），能够防止过拟合。让L2范数的规则项\(||W||_2\)最小，可以使得W的每个元素都很小，都接近于0，但与L1范数不同，它不会让它等于0，而是接近于0。越小的参数说明模型越简单，越简单的模型则越不容易产生过拟合现象。我也不懂，我的理解是：限制了参数很小，实际上就限制了多项式某些分量的影响很小（看上面线性回归的模型的那个拟合的图），这样就相当于减少参数个数。

l2的好处

• 学习理论的角度：

从学习理论的角度来说，L2范数可以防止过拟合，提升模型的泛化能力。

• 优化计算的角度：

从优化或者数值计算的角度来说，L2范数有助于处理 condition number不好的情况下矩阵求逆很困难的问题。

优化有两大难题，一是：局部最小值，二是：ill-condition病态问题。

ill-condition对应的是well-condition。那他们分别代表什么？假设我们有个方程组AX=b，我们需要求解X。如果A或者b稍微的改变，会使得X的解发生很大的改变，那么这个方程组系统就是ill-condition的，反之就是well-condition的。condition number就是拿来衡量ill-condition系统的可信度的。condition number衡量的是输入发生微小变化的时候，输出会发生多大的变化。也就是系统对微小变化的敏感度。如果一个矩阵的condition number在1附近，那么它就是well-conditioned的，如果远大于1，那么它就是ill-conditioned的。

如果方阵A是非奇异的(行列式不为0，又叫满秩矩阵)，那么A的conditionnumber定义为：

l2范数如何解决ill-conditioned问题：

常用图解释

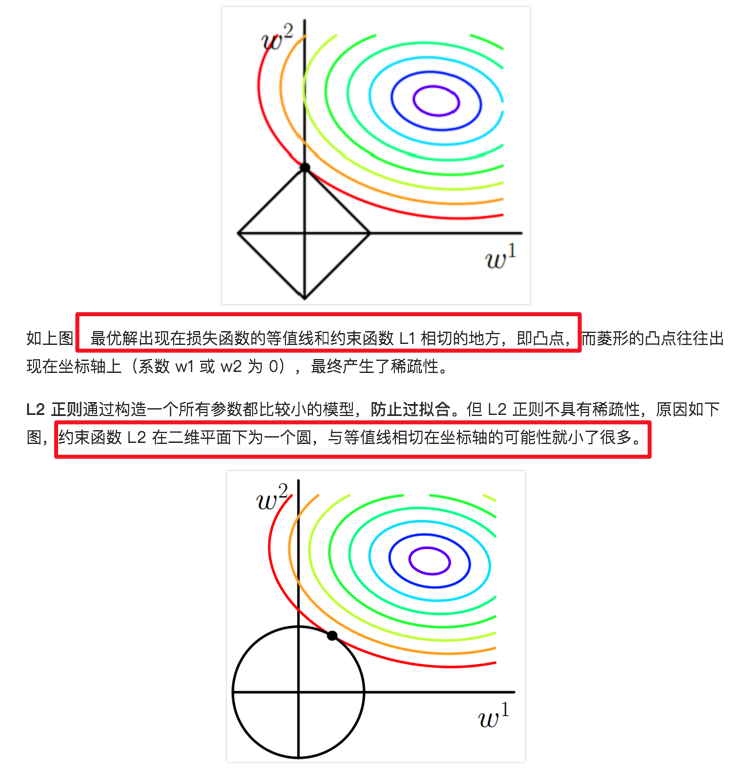
对于l1，a|w1| +b|w2| + c=0，假设a=b=1，c=-1 w1>0 w2>0，就有w1+w2-1=0==>w2=-w1+1，就是图中第一象限的那条直线， 同理w1>0,w2<0，w1-w2-1=0==>w2=w1-1，就是图中第四象限的直线， 同理w1<0,w2>0，-w1+w2-1=0==>w2=w1+1，第二象限 所以a|w1| +b|w2| + c=0是那个菱形的等高线 假设原来的损失函数是f(w1,w2)，就是图中的椭圆等高线

f(w1,w2)和a|w1|+b|w2|+c最先相交的点 就是w1=0,w2>0的时候，就是图中画的那个y轴上的点 而l2的最先的交点 不用w1取0，就可以相交了

不可导点的处理

使用Proximal Gradient Descent，参考https://www.cnblogs.com/breezedeus/p/3426757.html

西瓜书p252-254

整个loss变为soft thresholding：

\[ \text{prox}_{\mu g} (z) = \text{sign}(z) \max\{|z| - \mu, \ 0\} \]

上篇： pearson相关系数