目录

• 0. 推导
• 1. 最大间隔分类器
  • 1.1 logistic regression
  • 1.2 +1/-1分类
  • 1.3 函数间隔与几何间隔
    • 1.3.1 函数间隔(functional margin)\(\hat{\gamma}\)
    • 1.3.2 几何间隔(geometric margin)\(\tilde{\gamma}\)
    • 1.3.3 最大间隔分类器（maximum margin classifier）
  • 2. support vector
  • 3. kernel
  • 4. Outliers
  • 5. Numerical Optimization
  • 6. Duality
  • 7. Kernel II

参考:

• 支持向量机通俗导论（理解SVM的三层境界）：http://blog.csdn.net/v_july_v/article/details/7624837

• 支持向量机: Maximum Margin Classifier http://blog.pluskid.org/?p=632

• 支持向量机: Support Vector http://blog.pluskid.org/?p=682

• 支持向量机: Kernel http://blog.pluskid.org/?p=685

• 支持向量机：Outliers http://blog.pluskid.org/?p=692

• 支持向量机：Numerical Optimization http://blog.pluskid.org/?p=696

• 支持向量机：Duality http://blog.pluskid.org/?p=702

• 支持向量机：Kernel II http://blog.pluskid.org/?p=723

0. 推导

参考https://blog.csdn.net/u014433413/article/details/78427574

https://blog.csdn.net/lijil168/article/details/69395023

其中，\(L=1/2w^2+\sum _{i=1}^m\alpha _i[1-y_i(w^Tx+b)]\)，\(1-y_i(w^Tx+b)\)这项<=0，\(alpha\)>=0，所以\(L=1/2*w^2-CC\)，CC>=0，所以\(L<=1/2*w^2\)，\(max_{\alpha} L=1/2*w^2\)

原问题是\(min_{w,b}1/2*w^2\)，所以就是\(min_{w,b}max_{\alpha}L\)

1. 最大间隔分类器

1.1 logistic regression

0/1分类： 给sigmoid之前的函数值\(\theta^Tx\)是负无穷到正无穷，sigmoid之后的值相当于取y=1时的概率值，大于0.5就视为1的类。如果\(\theta^Tx>0\)则\(sigmoid(\theta^Tx)>0.5\)，换言之，要学到参数\(\theta\)，使正例的的\(\theta^Tx\)远大于0，负例的\(\theta^Tx\)远小于0.

1.2 +1/-1分类

svm中，使用+1/-1分类(方便推导公式)，而非logistic regression的0/1分类。

\[ g(f(x))=g(\omega^Tx+b) = \begin{cases} +1, \omega^Tx+b >= 0 \\ -1, \omega^Tx+b < 0 \\ \end{cases} \]

最简单的情形，假设数据是线性可分的。

所以，要寻找超平面的两条边界间的最大间隔，从而求w和b。

1.3 函数间隔与几何间隔

1.3.1 函数间隔(functional margin)\(\hat{\gamma}\)

函数间隔：\(\hat{\gamma}=y(\omega^Tx+b)=yf(x)\)（保证margin的非负）

超平面\((\omega,b)\)关于数据集T上的函数间隔：(w,b)关于T中所以样本点的函数间隔的最小值：

\[ \hat{\gamma}=min\hat{\gamma}_i,i=0,1,... \]

当w，b同时扩大时，超平面没变（\(\omega^Tx+b=0,2\omega^Tx+2b=0\)），但函数间隔却变大了，所以，需要规范化。

1.3.2 几何间隔(geometric margin)\(\tilde{\gamma}\)

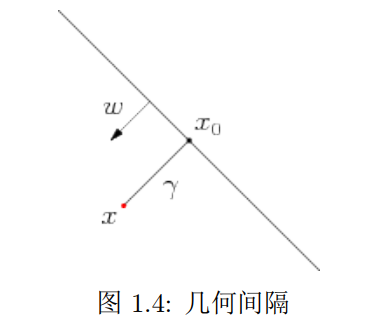
点\(x\)投影到超平面的点为\(x_0\),因为\(\omega\)是垂直于超平面的法向量，设\(x\)到超平面的距离是\(\gamma\),那么

\[ x=x_0+\gamma \frac{\omega}{||\omega||} \]

因为\(x_0\)是超平面上的点，所以\(f(x_0)=0\)，所以 \[ \\x=x_0+\gamma\frac{\omega}{||\omega||} \\\omega^Tx=\omega^Tx_0+\gamma\frac{\omega^T\omega}{||\omega||} \\\omega^Tx+b=\omega^Tx_0+b+\gamma\frac{\omega^T\omega}{||\omega||} \\f(x)=0+\gamma\frac{\omega^T\omega}{||\omega||} \\f(x)=\gamma||\omega|| \\\gamma=\frac{f(x)}{||\omega||} \]

因为\(\gamma\)也是有符号的，而间隔只要他的绝对值，所以，几何间隔定义为：

\[ \tilde{\gamma}=y\gamma=\frac{yf(x)}{||\omega||}=\frac{\hat{\gamma}}{||\omega||} \]

即，几何间隔＝函数间隔/\(||\omega||\)

1.3.3 最大间隔分类器（maximum margin classifier）

对一个数据点进行分类，当这个点和超平面之间的间隔越大的时候，分类正确的把握越大(离超平面越远，那他肯定不是分界面附近的点，肯定属于某一个类别)。对于一个包含n个点的数据集，我们可以很自然地定义它的间隔为所有这n个点的间隔中最小的那个。于是，为了使得分类的把握尽量大，我们希望所选择的超平面能够最大化这个间隔值（最大化这n个点里离超平面最近的点和超平面间的间隔）。

所以，最大间隔分类器的目标就是：

\[ \max\tilde{\gamma}, s.t. y_i(\omega^Tx_i+b)=\hat{\gamma}_i>=\hat{\gamma}, i=1,2,...,n \]

其中，\(\hat{\gamma}=\tilde{\gamma}||\omega||\)。

由于，即使超平面固定，\(\hat{\gamma}\)也会随着\(||\omega||\)的变化而变化，而我们的目标是固定超平面，所以可以固定\(\hat{\gamma}\)也可以固定\(||\omega||\)。为了方便推导，这里选择固定\(\hat{\gamma}\)。令\(\hat{\gamma}=1\)，则\(\tilde{\gamma}=\frac{1}{||\omega||}\)，所以，优化目标转化为：

\[ \max\frac{1}{||\omega||}, s.t. y_i(\omega^Tx_i+b)=\hat{\gamma}_i>=1, i=1,2,...,n \]

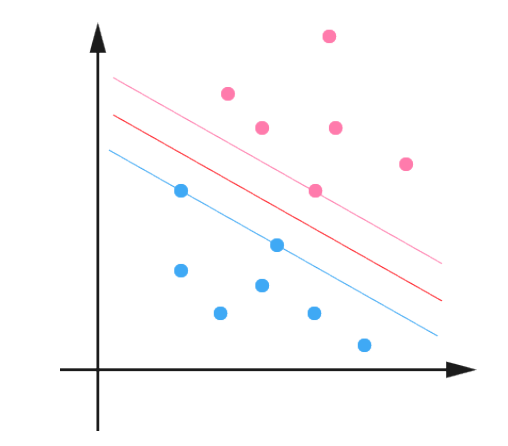
图中，红色和蓝色两个超平面到中间的超平面的距离都是\(\tilde{\gamma}\)，当这个分类间隔最大的时候，这两个超平面上的点都叫做support vector,满足\(y(\omega^Tx+b)=1\)，而非support vector的点，都有\(y(\omega^Tx+b)>1\)。

2. support vector

support vector的一个最直接的好处就是计算和存储上的优越性，几百万个点，实际上可能只有一两百个surpport vector，存储这一两百个点拿来做inference之类的就够了。

3. kernel

4. Outliers

5. Numerical Optimization

6. Duality

7. Kernel II

上篇： regularization相关