目录

• 1. 基于值函数逼近的理论讲解
• 2. DQN及其变种
  • 2.1 DQN方法
    • 2.1.1 利用深度卷积神经网络逼近行为值函数
    • 2.1.2 在强化学习的学习过程中引入经验回放
    • 2.1.3 设立了独立的目标网络单独处理时间差分算法中的TD偏差
    • DQN小结（by daiwk）
  • 2.2 Double DQN
    • 2.2.1 Qlearning的过估计
  • 2.3 优先回放(Prioritized Replay)
  • 2.4 Dueling DQN
• 3. 函数逼近方法
  • 3.1 基于非参数的函数逼近
    • 基于核函数的方法
    • 基于高斯过程的函数逼近方法
  • 3.2 基于参数的函数逼近
  • 3.3 卷积神经网络
    • 3.3.1 卷积运算
      • 稀疏连接
      • 权值共享
    • 3.3.2 池化
• 4. 各种其他优化

参考《深入浅出强化学习》

1. 基于值函数逼近的理论讲解

2. DQN及其变种

2.1 DQN方法

DeepMind发表在Nature上的文章Human-level control through deep reinforcement learning

最主要创新点是两个：

• 经验回放
• 设立单独的目标网络

大体框架是复用传统强化学习里的Qlearning方法。Qlearning包括两个关键点：

• 异策略：行动策略与 要评估的策略不是同一个策略。
  • 行动策略（用来选择行动$a$的策略）是$\epsilon -greedy$策略
  • 要评估和改进的策略是贪婪策略（即$max_aQ(s_{t+1},a)$，当前状态$s_{t+1}$下，使用各种a使$Q(s_{t+1},a)$达到的最大值），即，是最大的$Q$，与行动策略里随机选一个$a$得到的$Q$不同
• 时间差分（temporal difference, TD）：使用时间差分目标（即，$r_t+\gamma max_aQ(s_{t+1},a)$）来更新当前的行为值函数

注意，时间差分方法其实包括了异策略和同策略两种，

• 异策略(即off-policy)，如Qlearning，
• 同策略如Sarsa强化学习算法 （行为策略和目标策略都是$\epsilon$ -greedy策略）(书p77-79)

Qlearning的算法流程如下：

1. 初始化$Q(s,a),\forall s\in S,a\in A(s)$，给定参数$\alpha, \gamma$
2. Repeat
   1. 给定起始状态$s$，并根据$\epsilon -greedy$策略在状态$s$选择动作$a$
   2. Repeat
      1. 根据$\epsilon -greedy$策略选择动作$a_t$，得到回报$r_t$和下一个状态$s_{t+1}$
      2. 使用时间差分方法更新行为值函数$Q(s_t,a_t)\leftarrow Q(s_t,a_t)+\alpha [r_t+\gamma max_a(Q(s_{t+1},a))-Q(s_t,a_t)]$
      3. $s=s'$, $a=a'$
   3. Until $s$是最终状态
3. Until 所有的$Q(s,a)$收敛
4. 输出最终策略：$\pi (s)=argmax_aQ(s,a)$

DQN对Qlearning主要进行了如下三个修改：

• 利用深度卷积神经网络逼近行为值函数
• 在强化学习的学习过程中引入经验回放
• 设立了独立的目标网络单独处理时间差分算法中的TD偏差

2.1.1 利用深度卷积神经网络逼近行为值函数

行为值函数$Q(s,a)$用参数为$\theta$的非线性参数逼近$Q(s,a;\theta)$来近似

2.1.2 在强化学习的学习过程中引入经验回放

其实20世纪90年代就已经有用神经网络逼近行为值函数的方法了，但常常出现不稳定不收敛的情况。

deepmind的创始人Hassabis是神经科学的博士，他是研究人类大脑中负责记忆和学习的主要部分——海马体的。在人类睡觉时，海马体会把一天的记忆重放给大脑皮层。

训练神经网络时，存在的假设是训练数据是独立同分布的，但通过强化学习采集的数据间存在关联性，利用这些数据进行训练，神经网络就不会稳定。而经验回放就可以打破数据间的关联。

2.1.3 设立了独立的目标网络单独处理时间差分算法中的TD偏差

经验回放的技巧可以打破数据间的关联性，这个技巧在2013年的NIPS已经发布了，而2015年的Nature论文进一步提出了目标网络，进一步降低数据间的关联性。

正常的Qlearning更新值函数的方法如下：

$$Q(s_t,a_t)\leftarrow Q(s_t,a_t)+\alpha [r_t+\gamma max_a(Q(s_{t+1},a))-Q(s_t,a_t)]$$

但现在使用卷积神经网络来逼近，所以需要更新的是参数$\theta$，使用的方式自然是梯度下降：

$$\theta_{t+1}=\theta _t+\alpha [r+\gamma max_{a'}(Q(s',a';\theta))-Q(s',a';\theta)]\nabla Q(s,a;\theta)$$

而这里的$r+\gamma max_{a'}(Q(s',a';\theta))$是TD目标，在计算$max_{a'}(Q(s',a';\theta))$时用到的网络参数为$\theta$。

在DQN之前，计算TD目标的动作值函数所用的网络参数$\theta$与梯度计算中要逼近的动作值函数所用的网络参数相同，这样就容易导致数据间存在关联性，从而使训练不稳定。

所以DQN的做法就是将TD目标的网络表示为$\theta ^{-}$，用于动作值函数逼近的网络$\theta$每一步都更新，而用于计算TD目标的网络$\theta ^{-}$则是每固定的步数才更新一次【这就可以使得在一段时间里目标Q值是保持不变的，从而使得在一段时间里能集中力量去优化真正的目标$\theta$，等真正的目标好一点了，再去更新$\theta^-$】：

$$\theta_{t+1}=\theta _t+\alpha [r+\gamma max_{a'}(Q(s',a';\theta ^{-}))-Q(s,a;\theta)]\nabla Q(s,a;\theta)$$

DQN的训练算法如下：

1. 初始化replay memory $D$，capacity设为$N$
2. 使用随机权重$\theta$初始化动作值函数$Q$
3. 使用权重$\theta^{-}=\theta$初始化目标动作值函数$\hat {Q}$
4. For $episode = [1,...,M]$ do
   1. 初始化事件的第一个状态($x_1$是第一张图片)$s_1=\{x_1\}$，并通过预处理得到状态对应的特征输入$\phi _1=\phi(s_1)$
   2. For $t=[1,...T]$ do
      1. 根据概率$\epsilon$随机选择一个动作$a_t$
      2. 如果小概率事件没有发生，就用贪婪策略选择当前行为值函数最大的那个动作：$a_t=argmax_a(Q(\phi(s_t),a;\theta))$【上面那行和这行就是所谓的行动策略，$\epsilon -greedy$策略】
      3. 在模拟器中执行动作$a_t$，得到回报$r_t$以及图片$x_{t+1}$
      4. 令$s_{t+1}=s_t,a_t,x_{t+1}$，然后预处理$\phi _{t+1}=\phi(s_{t+1})$
      5. 将transition $(\phi_t,a_t,r_t,\phi _{t+1})$存入$D$。
      6. 从$D$中随机sample出一个minibatch的transitions，$(\phi _j,a_j,r_j,\phi _{j+1})$
      7. 令$y_j=\left\{\begin{matrix}r_j & if\ episode\ terminates\ at\ step\ j+1\\ r_j+\gamma max_{a'}\hat {Q}(\phi_{j+1},a';\theta^{-}) & otherwise \end{matrix}\right.$
      8. 对$(y_j-Q(\phi _j,a_j;\theta))^2$的参数$\theta$进行一个梯度下降step的更新，$\theta_{t+1}=\theta _t+\alpha [r+\gamma max_{a'}(\hat {Q}(s',a';\theta ^{-}))-Q(s,a;\theta)]\nabla Q(s,a;\theta)$
      9. 每$C$个step，令$\hat {Q}=Q$，即令$\theta ^{-}=\theta$
   3. End For
5. End For

DQN小结（by daiwk）

• 算$y_i$的时候用的是目标网络$\hat{Q}$和$\theta ^-$
• loss是目标网络算出来的$r+\gamma max \hat{Q}$与原网络$Q$之差
• $y_i$是当前reward，基于状态$s_{t+1}$再执行一个action得到的新的reward。而原网络$Q$是当前的状态$s_t$。
• 总共有这么几大步：
  • 当前状态$s_t$，处理后是$\phi _t$，通过$\epsilon -greedy$得到$Q$最大的$a_t$
  • 执行$a_t$，得到$\phi _t, a_t,r_t,\phi_{t+1}$，扔进replay buffer中
  • 采样出一个$\phi _j,a_j,r_j,\phi_{j+1}$
  • 计算在$\phi _{j+1}$上再执行一个使得$\hat {Q}$(注意，这里不是$Q$)最大的动作$a'$得到的reward：$y_j=r_j+\gamma max \hat {Q}(\phi_{j+1},a')$
  • 算$y_i$和当前$Q$的残差，梯度下降，更新当前$Q$的参数：$\theta += \alpha (y_j-Q)\nabla Q$
  • $C$步之后，把当前$Q$的参数赋值给$\hat {Q}$
• 再次强调
  • $maxQ$的是当前状态+当前动作；
  • $max\hat {Q}$是下一状态+下一动作；
  • 用来算残差的也是当前状态+当前动作得到的$Q$

2.2 Double DQN

2.2.1 Qlearning的过估计

DQN无法克服Qlearning本身固有的缺点：过估计

过估计指的是估计的值函数比真实值函数大，Qlearning出现过估计的问题，根源在于其中的最大化操作：

对于表格型，值函数评估的更新公式：

$$Q(s_t,a_t)\leftarrow Q(s_t,a_t)+\alpha [r_t+\gamma \underset{a}{max}Q(s_{t+1},a)-Q(s_t,a_t)]$$

对于基于函数逼近的方法，值函数更新公式为：

$$\theta _{t+1}=\theta_t+\alpha(R_{t+1}+\gamma \underset{a}{max}Q(S_{t+1},a;\theta_t)-Q(S_t,A_t;\theta_t))\triangledown _{\theta_t}Q(S_t,A_t;\theta_t)$$

可以发现不管是表格型，还是基于值函数逼近的方法，更新公式中都有max操作，使得估计的值函数比值函数的真实值大。

如果过估计是均匀的，即值函数的每一点的值都被过估计了相同的幅度，那么由于最优策略是贪婪策略，即找最在的值函数所对应的动作，在这种情况下一不会影响最优策略（因为每个值函数都变大一样的幅度，所以原来最大的那个还是最大），这样因为强化学习的目标是找到最优策略，所以不会影响我们解决问题~

但实际情况中，过估计量并不是均匀的，所以会影响最终策略，使得最终策略并非最优！！

在Qlearning的值函数更新中，TD目标为：

$$Y^Q_t=R_{t+1}+\gamma max_aQ(S_{t+1},a;\theta_t)$$

• 动作选择

在求TD目标$Y^Q_t$时，首先需要选择一个动作$a^*$，该动作$a^*$应该满足在状态$S_{t+1}$处使得$Q(s_{t+1},a)$最大，这就是动作选择。

• 动作评估

选出$a^*$后，利用$a^*$处的动作值函数构造TD目标。

一般的Qlearning使用同一个参数$\theta_t$来选择和评估动作。

Double Qlearning将动作的选择和动作的评估分别用不同的值函数来实现，从而其TD目标为：

$$Y^{DoubleQ}_t=R_{t+1}+\gamma Q(S_{t+1},argmax_aQ(S_{t+1},a;\theta_t);\theta_t')$$

所以，我们可以看出，动作的选择所选择的$a^*$为

$$a^*=argmax_aQ(S_{t+1},s;\theta_t)$$

动作值函数网络的参数是$\theta_t$。当选出最大动作$a^*$之后，动作评估的公式为：

$$Y^{DoubleQ}_t=R_{t+1}+\gamma Q(S_{t+1},a^*;\theta_t')$$

所以，引入DQN就是Double DQN：

Deep Reinforcement Learning with Double Q-learning

将TD error修改为：

$$r+\gamma Q(s',argmax_{a'}Q(s',a',\theta),\theta^-)-Q(s,a,\theta)$$

其中

• $\theta$是当前的网络参数，用来选择动作
• $\theta^-$是前一步的网络参数（$delayed \theta$），用来评估动作

因为原来的DQN就已经引入了目标网络$\theta^-$，所以其实改动不大。 但注意！！区别在于，原来DQN的TD error是$r+\gamma Q(s',argmax_{a'}Q(s',a',\theta^-),\theta^-)$，即动作选择和动作评估都是$\theta^-$。而Double DQN动作选择是$\theta$，动作评估是$\theta^-$

2.3 优先回放(Prioritized Replay)

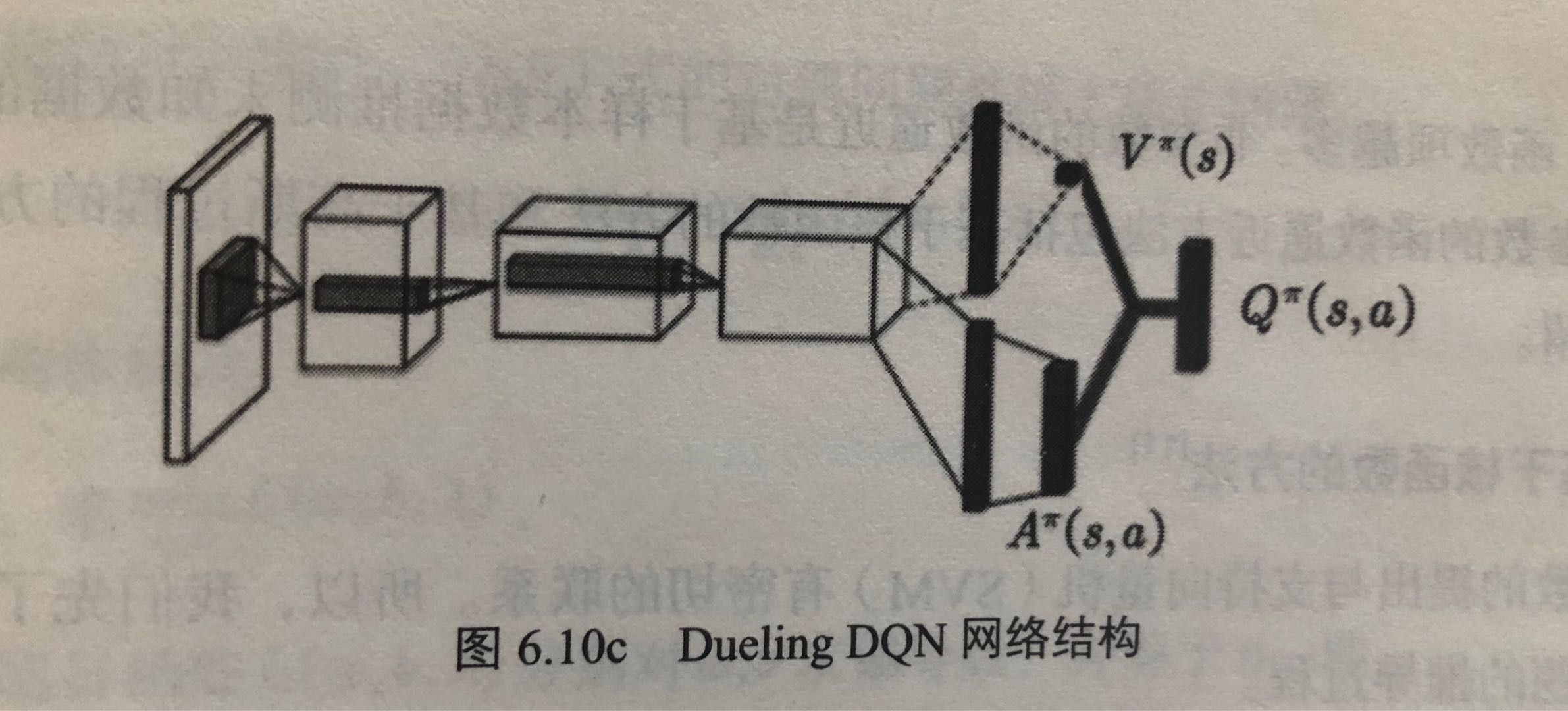
2.4 Dueling DQN

参考书本，以及https://blog.csdn.net/u013236946/article/details/73161586

竞争网络（dueling net）从网络结构上改进了DQN，将动作值函数分解为状态值函数和优势函数，即：

$$Q^{\pi}(s,a)=V^{\pi}(s)+A^{\pi}(s,a)$$

以往的DQN都是直接用神经网络逼近$Q^{\pi}(s,a)$，而Dueling DQN则是对$V^{\pi}(s)$和$A^{\pi}(s,a)$分别用神经网络来逼近。

• 状态值函数$V^{\pi}(s)$表示静态的状态环境本身具有的价值。是一个scalar。
• 依赖状态的动作优势函数$A^{\pi}(s,a)$(advantage function)，表示选择某个Action额外带来的价值。是一个vector。

更详细地，状态价值函数表示为

$$V(s;\theta,\beta)$$

动作优势函数表示为

$$A(s,a;\theta,\alpha)$$

动作Q值为两者相加

$$Q(s,a;\theta,\alpha,\beta) = V(s;\theta,\beta)+A(s,a;\theta,\alpha)$$

其中，$\theta$是卷积层的参数，$\beta$和$\alpha$是两个支路全连接层的参数。

而在实际中，一般要将动作优势流设置为单独动作优势函数减去某状态下所有动作优势函数的平均值，这样做可以保证该状态下各动作的优势函数相对排序不变，而且可以缩小Q值的范围，去除多余的自由度，提高算法稳定性。

$$Q(s,a;\theta,\alpha,\beta) = V(s;\theta,\beta)+(A(s,a;\theta,\alpha)-\frac{1}{|A|}\sum_{a'}A(s,a';\theta,\alpha))$$

这种竞争结构能学到在没有动作的影响下环境状态的价值$V(s)$。如下图，在训练过程中，上下两行图表示不同时刻，左右两列表示属于$V(s)$和$A(a)$，（通过某种方法处理后）图中红色区域代表$V(s)$ 和$A(a)$所关注的地方。$V(s)$关注于地平线上是否有车辆出现（此时动作的选择影响不大）以及分数；$A(a)$则更关心会立即造成碰撞的车辆，此时动作的选择很重要。

论文中dueling net结合了DDQN(double dqn)以及优先级采样（Prioritized Experience Replay）的训练方式。

3. 函数逼近方法

3.1 基于非参数的函数逼近

基于核函数的方法

基于高斯过程的函数逼近方法

3.2 基于参数的函数逼近

3.3 卷积神经网络

3.3.1 卷积运算

稀疏连接

权值共享

3.3.2 池化

4. 各种其他优化

参考https://zhuanlan.zhihu.com/p/21547911

几个问题：

• 目标Q值的计算准确吗？全部通过max Q来计算有没有问题？
• 随机采样的方法好吗？按道理不同样本的重要性是不一样的
• Q值代表状态，动作的价值，那么单独动作价值的评估会不会更准确？
• DQN中使用$\epsilon-greedy$的方法来探索状态空间，有没有更好的做法？
• 使用卷积神经网络的结构是否有局限？加入RNN呢？
• DQN无法解决一些高难度的Atari游戏比如Montezuma’s Revenge，如何处理这些游戏？
• DQN训练时间太慢了，跑一个游戏要好几天，有没有办法更快？
• DQN训练是单独的，也就是一个游戏弄一个网络进行训练，有没有办法弄一个网络同时掌握多个游戏，或者训练某一个游戏后将知识迁移到新的游戏？
• DQN能否用在连续动作输出问题？

解法：

• 改进目标Q值计算：Deep Reinforcement Learning with Double Q-learning
• 改进随机采样：Prioritized Experience Replay
• 改进网络结构，评估单独动作价值：Dueling Network Architectures for Deep Reinforcement Learning ( 本文为ICML最佳论文之一）
• 改进探索状态空间方式：（1）Deep Exploration via Bootstrapped DQN （2）Incentivizing Exploration In Reinforcement Learning With Deep Predictive Models
• 改变网络结构，增加RNN：Deep Recurrent Q-Learning for Partially Observable MDPs（非DeepMind出品，效果很一般，谈不上改进，不考虑讲解）
• 实现DQN训练的迁移学习：（1）Policy Distillation （2） Actor-Mimic: Deep Multitask and Transfer Reinforcement Learning
• 解决高难度游戏Montezuma‘s Revenge：Unifying Count-Based Exploration and Intrinsic Motivation
• 加快DQN训练速度：Asynchronous Methods for Deep Reinforcement Learning（这篇文章还引出了可以替代DQN的A3C算法，效果4倍Nature DQN）
• 改变DQN使之能够应用在连续控制上面：Continuous Deep Q-Learning with Model-based Acceleration

上篇： multi-task learning